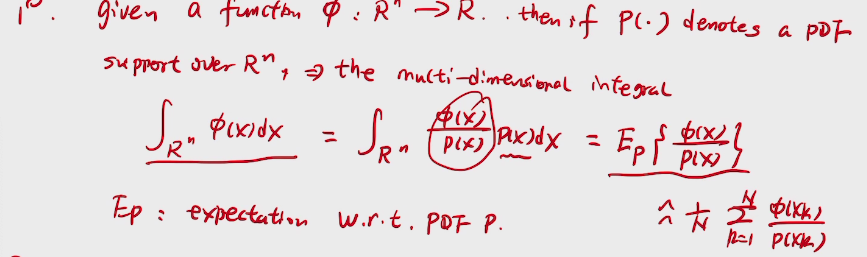[RL] Probability Review
Basics
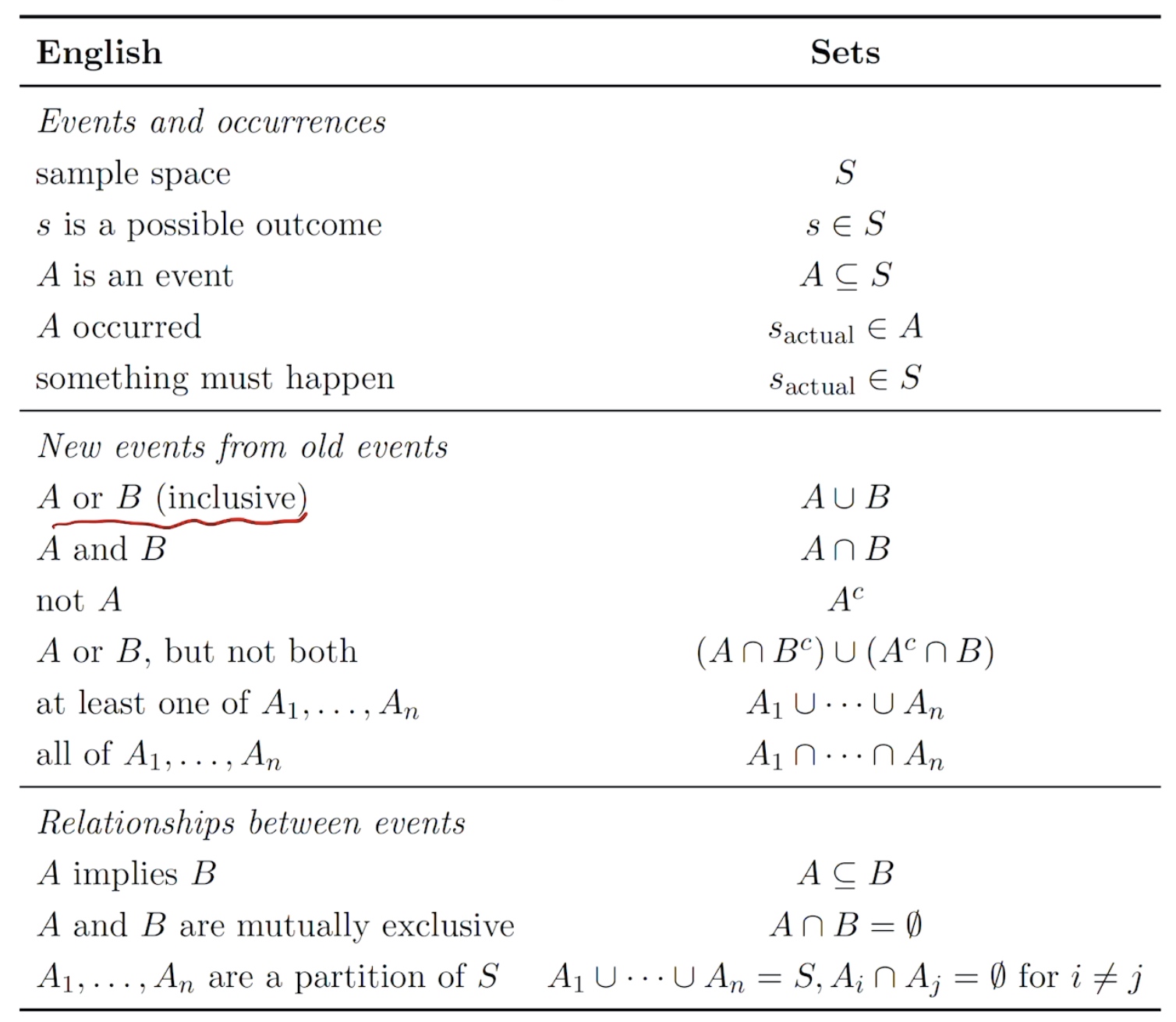
The set
general definition of Probability
样本空间
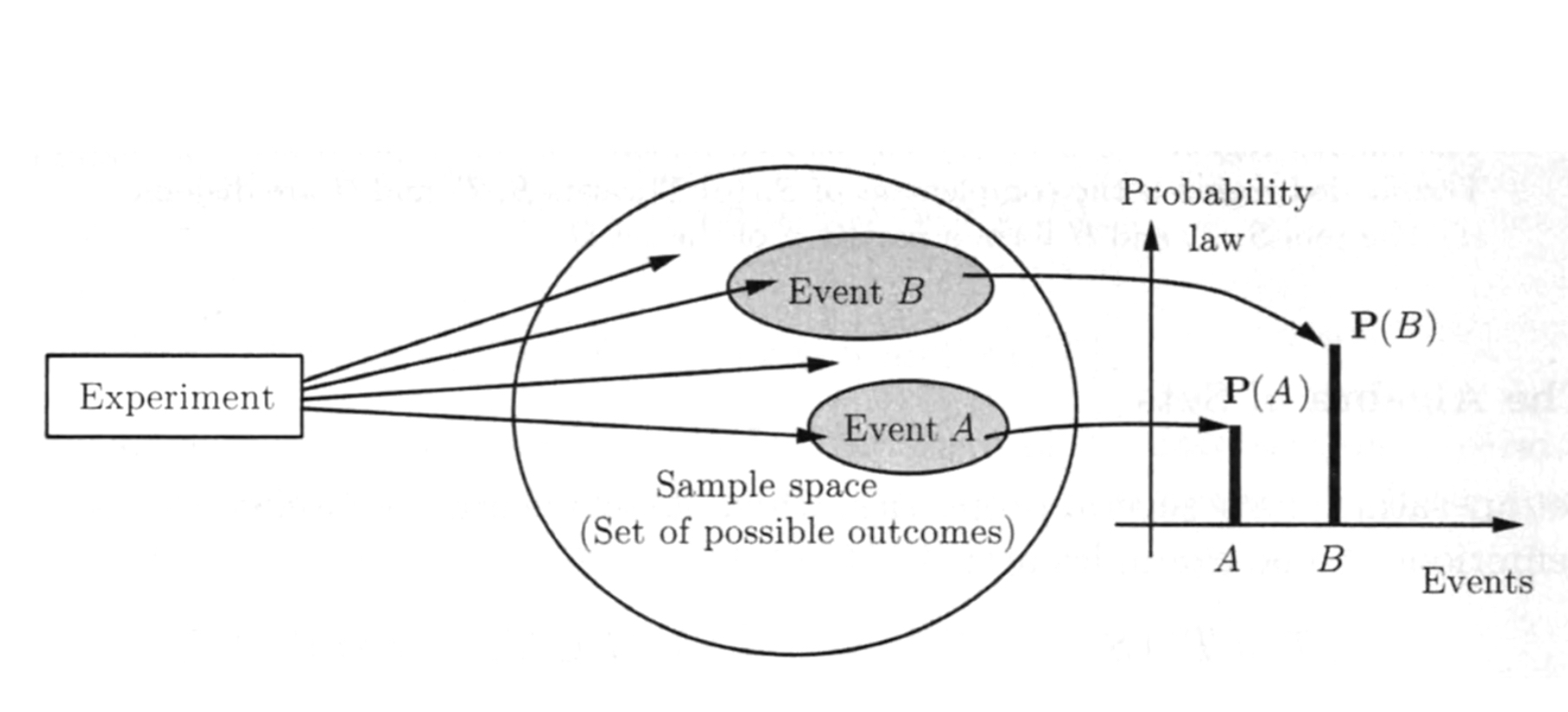
概率的物理意义
frequentist view: a long-run frequency over a large number of repetitions of an experiment.
Bayesian view: a degree of belief about the event in question.
We can assign probabilities to hypotheses like "candidate will win the election" or "the defendant is guilty"can't be repeated.
Markov & Monta Carlo + computing power + algorithm thrives the Bayesian view.
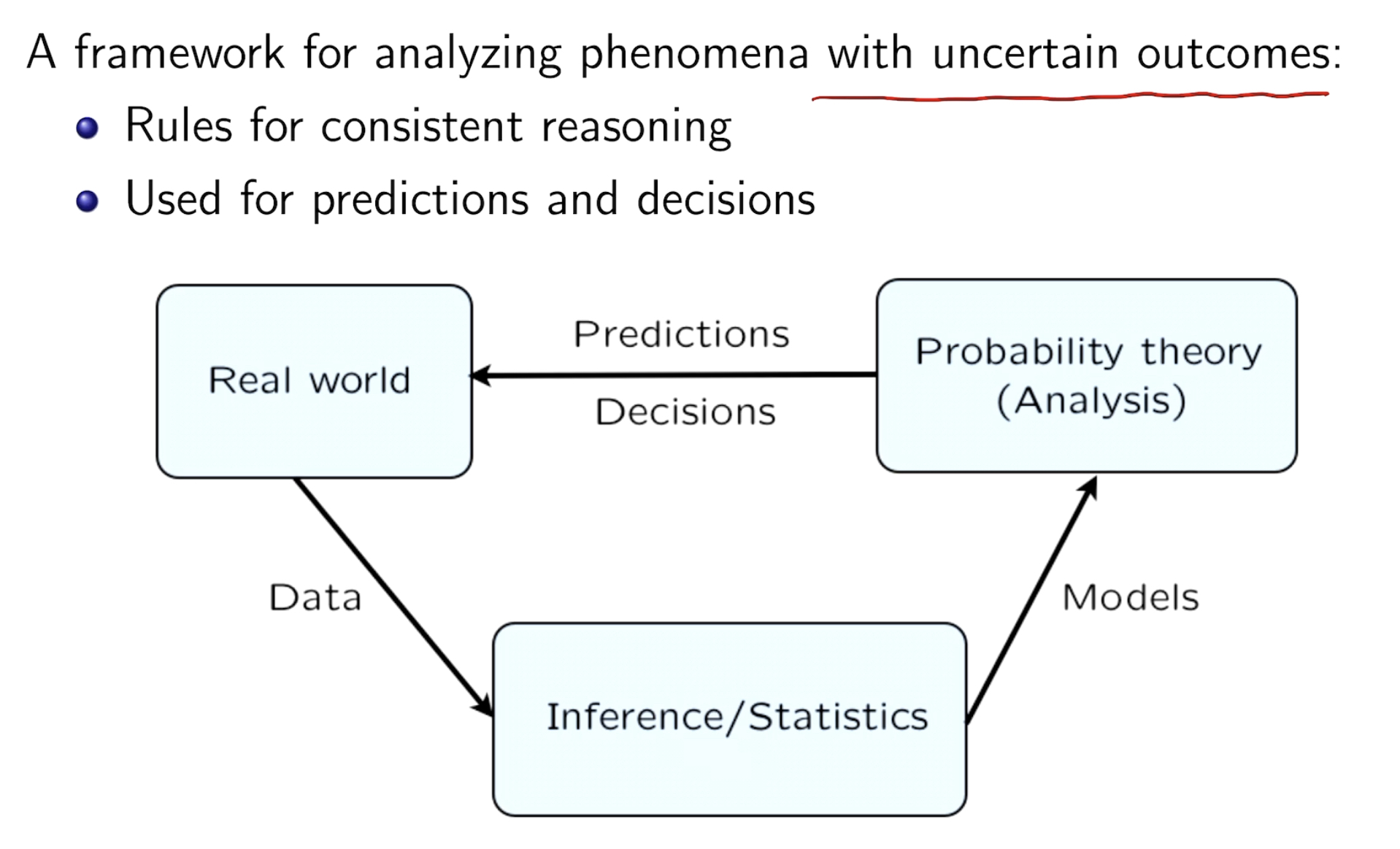
role
条件概率
所有事情都有条件,条件就会产生概率
e.g. Conditioning -> DIVIDE & CONCUER -> recursively apply to multi-stage problem.
P(A|B) = \(\frac{P(A\ and\ B)}{P(B)}\)
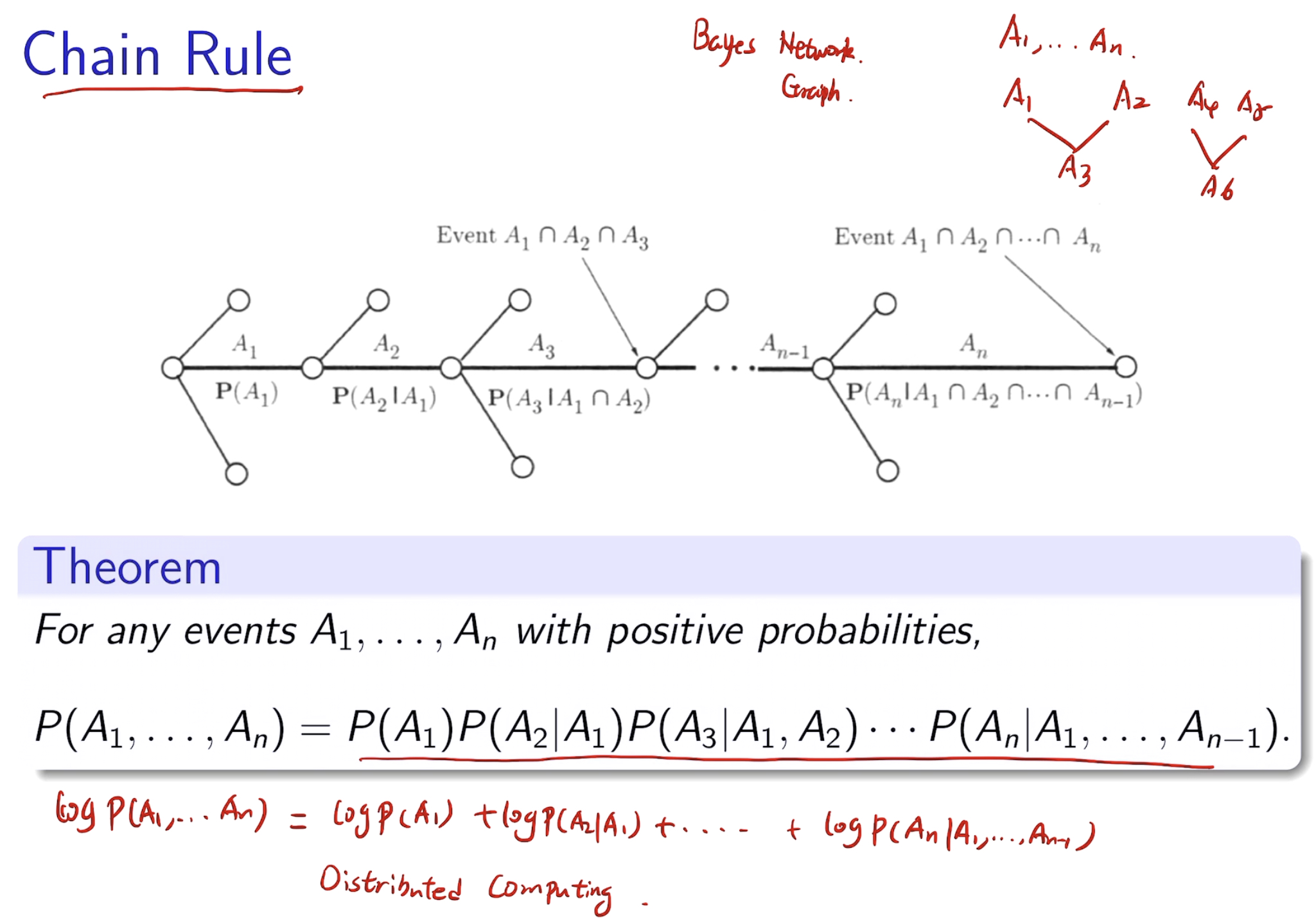
chain rules
有利于分布式计算
Inference & Bayes' Rules
概率分布和极限定理
PDF 概率密度函数
混合型

valid PDF
- non negative \(f(x)\geq0\)
- integral to 1:
\(\int^{\infty}_{-\infty}f(x)dx=1\)
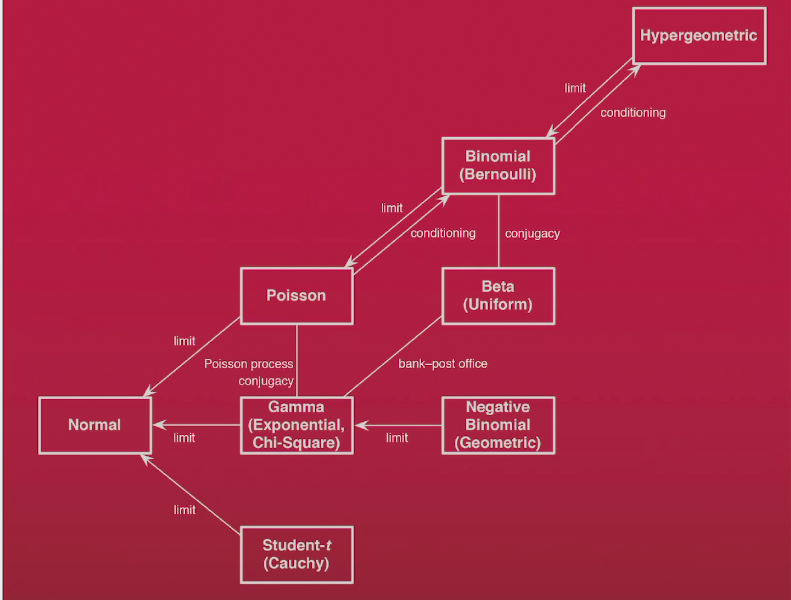
probability distribution
summary of probability distribution
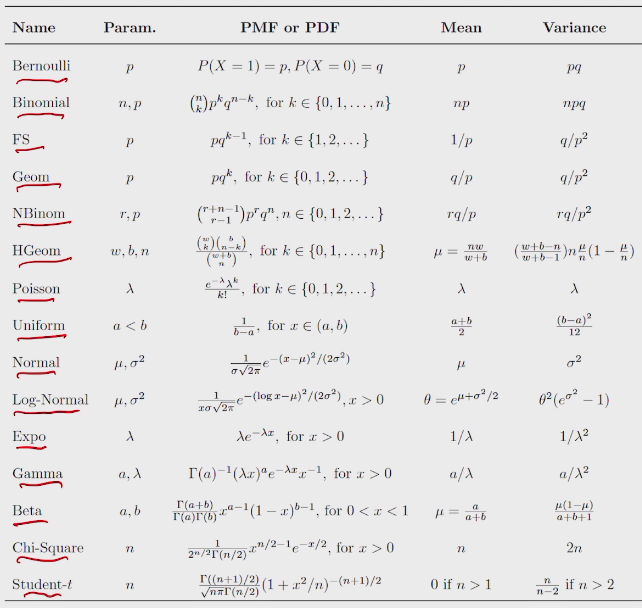
三种距离衡量 in ML, DL, AI
全变量距离
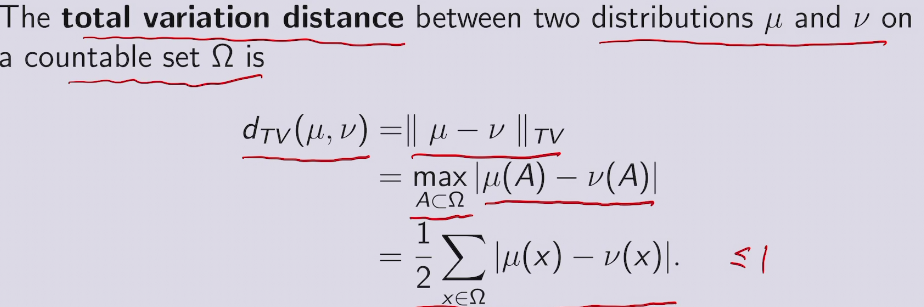
usually in GAN
小数定理(稀疏事件) in poisson

去食堂吃饭人数可以用柏松分布来描述
Sample mean
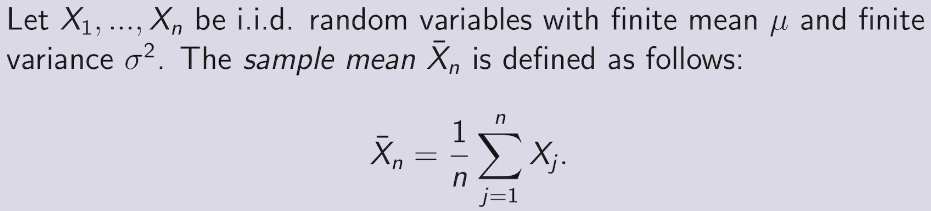
强大数定理SLLN

收敛到真正的概率值以概率为一收敛
弱大数定理WLLN
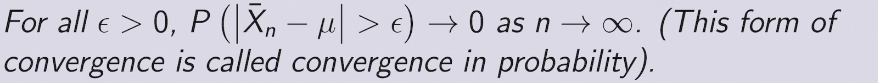
以概率收敛
中心极限定理

Generating function
- PGF - Z

- MGF - Laplace

- CF - 傅立叶
APPLICATION
- branching process
- bridge complex and probability
- play a role in large deviation theory
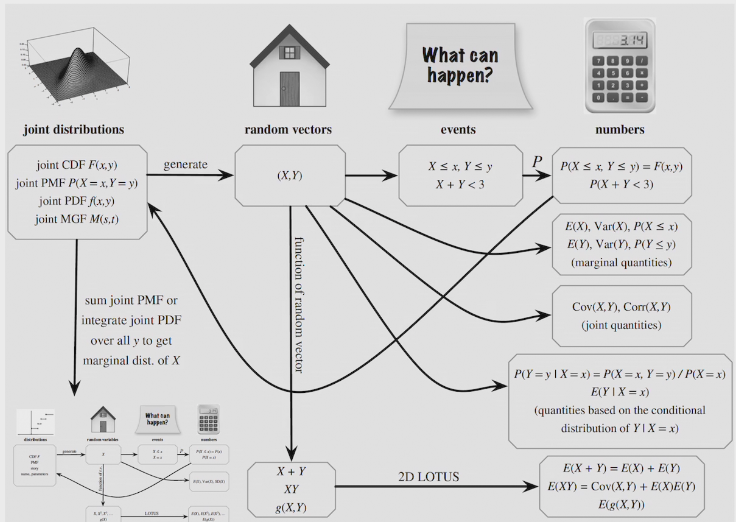
## Multi variables.
joint distribution provides complete information about how multiple r.v. interact in high-dimensional space

joint CDF &PDF
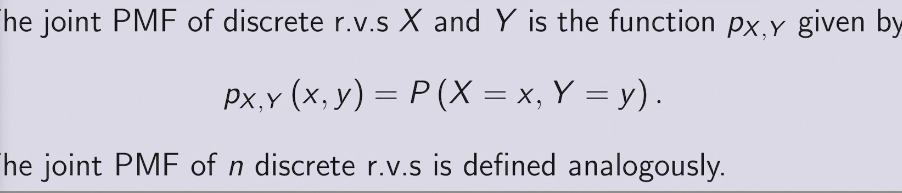
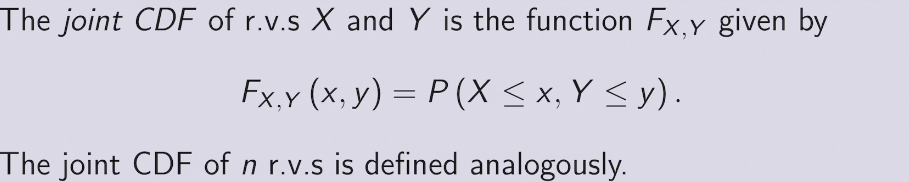
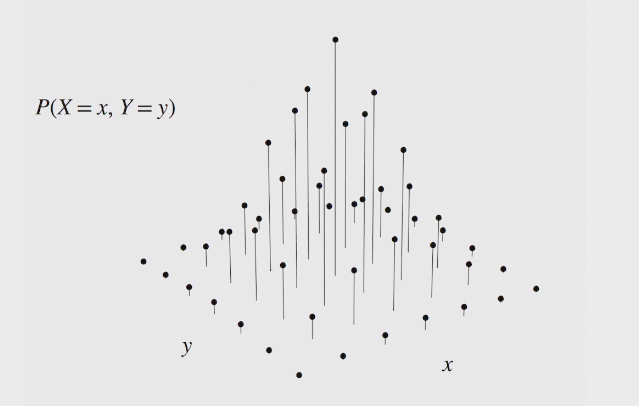
marginal PMF
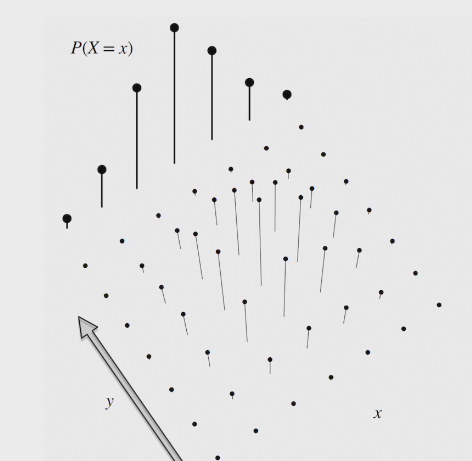
conditional PMF
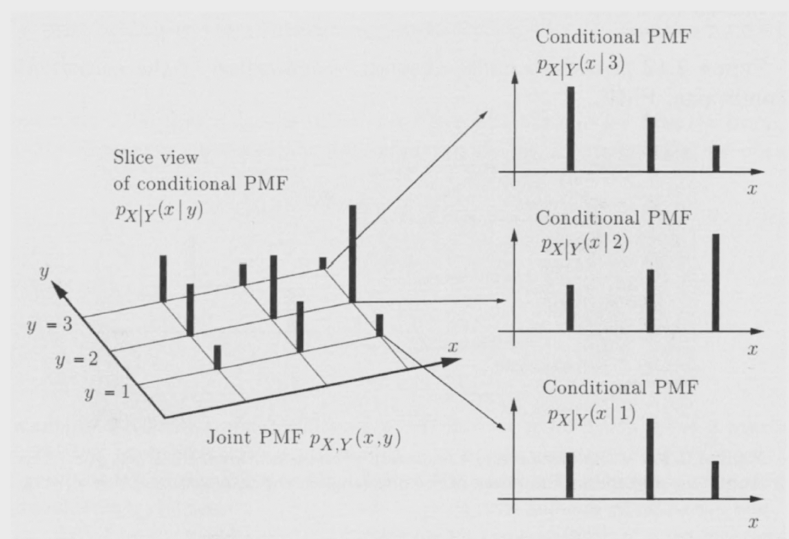
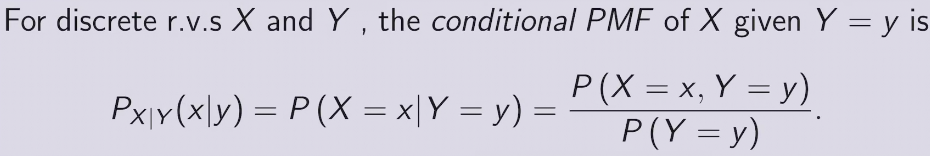
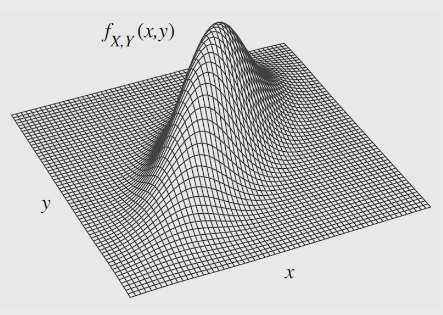
joint PDF
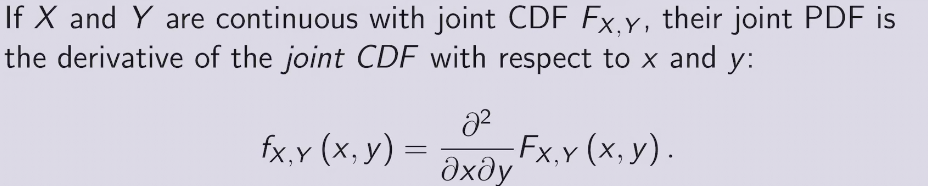
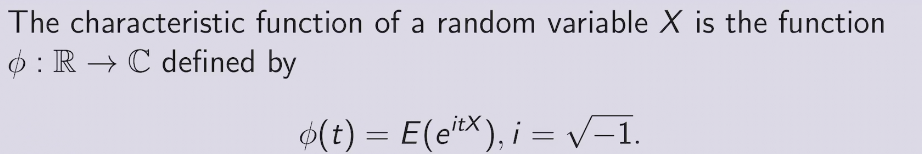
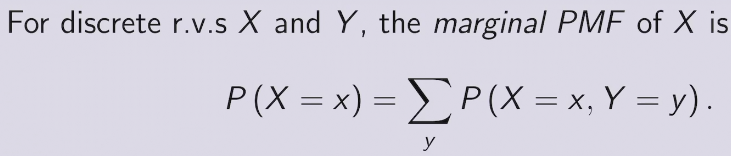
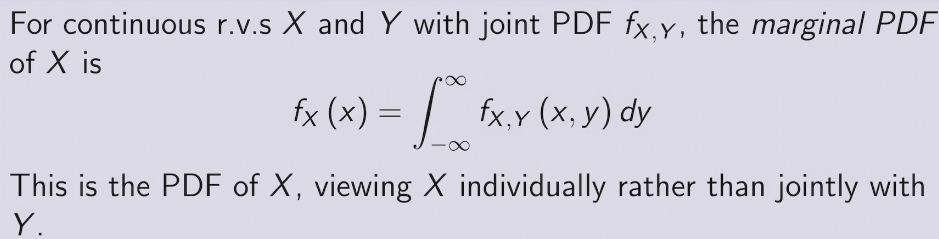
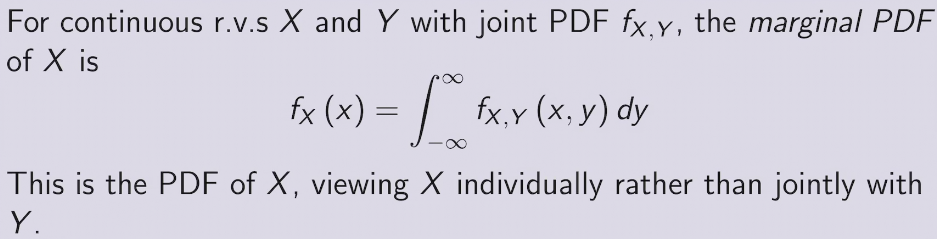
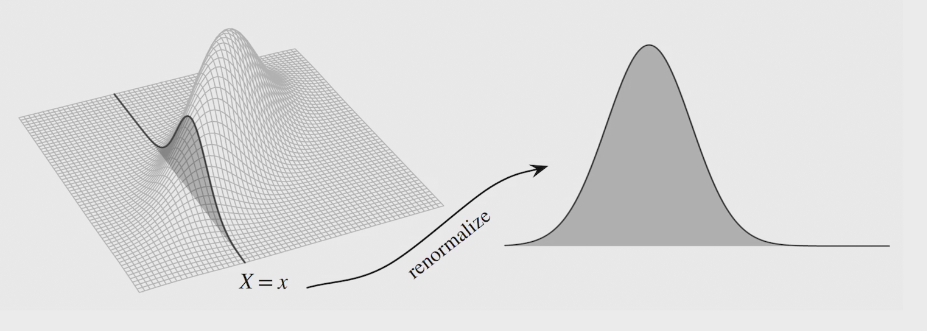
techniques

general Bayes' Rules.

general LOTP

change of variables

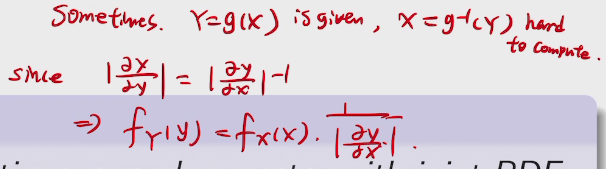
summary

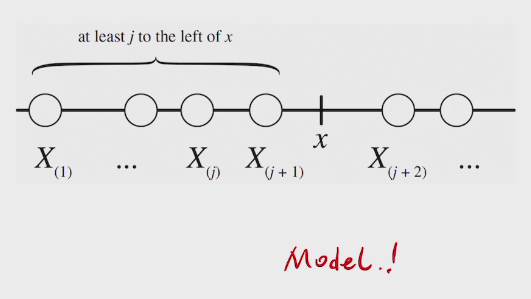
Order Statistics
CDF of order statistic
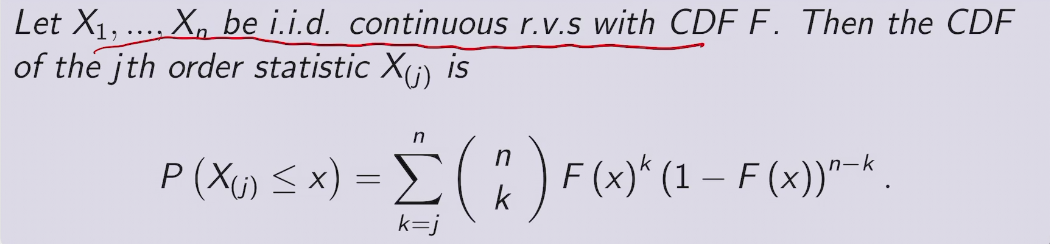
proof
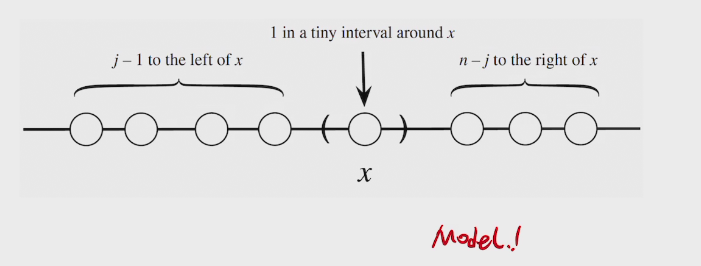
PDF of Order Statostic

two methods to find PDF
- CDF -differentiate> PDF (ugly)
- PDF*dx

###proof
## joint PDF
e.g. order statistics of Uniforms
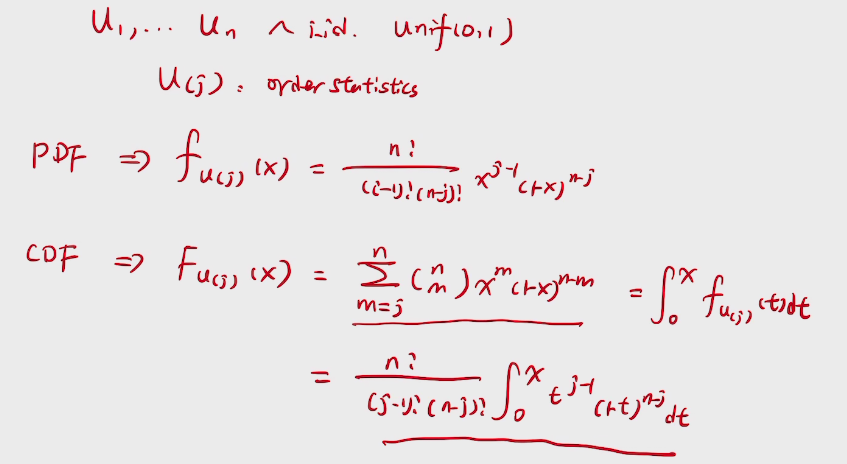
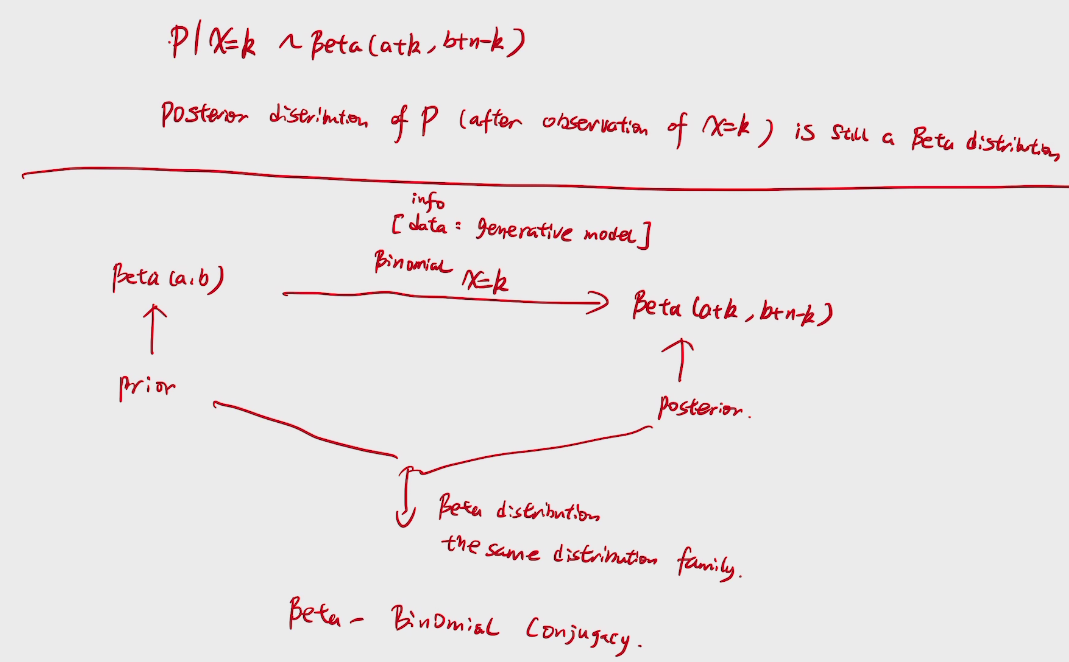
story:beta-Binomial Conjugacy

Mean vs Bayes'

deduction

e.g. 拉普拉斯问题
来自大名鼎鼎的拉普拉斯的问题,若给定太阳每天都升起的历史记录,则太阳明天仍然能升起的概率是多少?
拉普拉斯自己的解法:
假定太阳升起这一事件服从一个未知参数A的伯努利过程,且A是[0,1]内均匀分布,则利用已给定的历史数据,太阳明天能升起这一事件的后验概率为
\(P(Xn+1|Xn=1,Xn-1=1,...,X1=1)=\frac{P(Xn+1,Xn=1,Xn-1=1,...,X1=1)}{P(Xn=1,Xn-1=1,...,X1=1)}\)=An+1 在[0,1]内对A的积分/An 在[0,1]内对A的积分=\(\frac{n+1}{n+2}\),即已知太阳从第1天到第n天都能升起,第n+1天能升起的概率接近于1.
Monte carlo
importance sampling

reduce the 方差
importance sampling
example

What does Multi-Armed Bandit means?
credit:https://iosband.github.io/2015/07/19/Efficient-experimentation-and-multi-armed-bandits.html
At first, multi-armed bandit means using
\(f^* : \mathcal{X} \rightarrow \mathbb{R}\)
- Each arm \(i\) pays out 1 dollar with probability \(p_i\) if it is played; otherwise it pays out nothing.
- While the \(p_1,…,p_k\) are fixed, we don’t know any of their values.
- Each timestep \(t\) we pick a single arm \(a_t\) to play.
- Based on our choice, we receive a return of \(r_t \sim Ber(p_{a_t})\).
- ##How should we choose arms so as to maximize total expected return?##