[latexpage]

在之前的 adversarial example 框架下，赵博又让我把模型转化成pb格式给这个论文转化的工具用，应该是之前的 baseline 跑数据太稳定了。

感谢这次学长给我的这个锅还是非常轻松的，因为这周去找高中同学吃饭，又和老婆玩，实在没时间，ddl太多。还得复习。

credit：https://blog.csdn.net/kearney1995/article/details/79904095

由于之前提出的防御性蒸馏实际上是一种"梯度遮蔽"的方法，作者也给出了防御性蒸馏有效性的解释。这里所说的蒸馏学习是原先hinton提出用来减少模型复杂度并且不会降低泛化性能的方法，具体就是在指定温度下，先训练一个教师模型，再将教师模型在数据集上输出的类别概率标记作为软标签训练学生模型。而在防御蒸馏模型中，选择两个相同的模型作为教师模型和学生模型。 

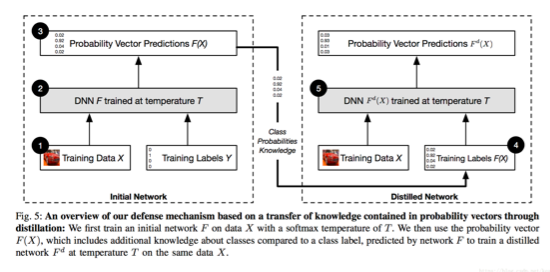
具体过程：

1、 先用硬标签训练教室模型，在文中的例子就是假设温度为T，则教室模型的Softmax层输出F（X）就是

\begin{equation}\nonumber F(X)=\Big[{e^{z_i(X)/T} \over {\sum_{l=0}^{N-1} e^{z_l(X)/T}}} \Big]_{i \in 0 \dots N-1} \end{equation}

再此基础上应用交叉熵损失训练模型。

2、然后用教师模型输出类别概率F(X)（注意，这里还是保持了温度T）实际上，这和T=1，即普通情况下训练模型，并没有什么太大区别，但我们还是与原文保持一致。

3、对于学生模型，我们还是利用温度T下的输出F(X)计算交叉熵损失函数，不过类别标签应用之前教师模型输出的软标签，进而进行训练。 对于使用软标签带来的好处，主要在于使用软标签F(X)使得神经网络能够在概率向量中找到的附加知识。 这个额外的熵编码了类之间的相对差异。 例如，在手写数字识别的背景下，给定一些手写数字的图像X，模型F可以评估数字7到F7(X)=0.6的概率以及标签1到F1(X)=0.4的概率，这表明7和1之间有一些结构相似性。

4、对于模型的预测输出，我们反而将温度T降为1，从而以高置信度来预测未知输入的类别。 实际上我们根本不需要前面的教师模型，只需要将F(X)作为神经网络的输出来最小化交叉熵损失函数既可以达到防御FGSM和JSMA的攻击。
  作者也对防御蒸馏的有效性进行的分析，对softmax层的输出求梯度可以很容易的得出：

\begin{equation}\nonumber \begin{aligned} {\partial F_i(X) \over \partial X_j}\Big|_T &= {\partial \over \partial X_j} \Big({e^{z_i/T} \over \sum_{l=0}^{N-1} e^{z_l/T}} \Big) \\ &= {1 \over g^2(X)} \Big({\partial e^{z_i(X)/T} \over \partial X_j}g(X)-e^{z_i(X)/T}{\partial g(X) \over \partial X_j} \Big) \\ &={1 \over g^2(X)}{e^{z_i/T} \over T}\Big(\sum_{l=0}^{N-1}{\partial z_i \over \partial X_j}e^{z_l/T}-\sum_{l=0}^{N-1}{\partial z_l \over \partial X_j}e^{z_l/T}\Big) \\ &={1 \over T}{e^{z_i/T} \over g^2(X)} \Big(\sum_{l=0}^{N-1}\big({\partial z_i \over \partial X_j}-{\partial z_l \over \partial X_j}\big) e^{z_l/T} \Big) \end{aligned} \end{equation}

这种攻击针对的就是LSTM法所做的优化，实际上完全无法攻击JSMA，C&W在优化后成功攻击该防御模型，若对防御蒸馏攻击的softmax的输出做梯度，得到的是零。所以这个操作的本质就是梯度遮蔽。

EAD: Elastic-Net Attacks to Deep Neural Networks via Adversarial Examples

中提到的就是Carlini & Wagner的一些新的改进

\begin{equation}\nonumber f(\boldsymbol{x},t) = \max \{\max_{j \neq t}[Logit(\boldsymbol{x})]_j - [Logit(\boldsymbol{x})]_t,-k\} \end{equation}

改变的目标函数依然没有变化。主要是加入了L1和L2弹性网络正则化项，之后只要做优化就OK

\begin{equation}\nonumber \begin{aligned} & \min_\boldsymbol{x} c \cdot f(\boldsymbol{x},t) + \beta ||\boldsymbol{x}-\boldsymbol{x}_0||_1 + ||\boldsymbol{x}-\boldsymbol{x}_0||_2^2 \\ & \text{s.t.} \quad \boldsymbol{x} \in [0,1]^p \end{aligned} \end{equation}

接下来就是数学问题了。

回归题目

作者也给出了防御性蒸馏有效性的解释，详见之前关于防御性蒸馏的文章，和那里面说的一样；不过关于jsma中选择像素对来进行修改的方法，作者做出了不一样的解释：
  假设softmax层最小的输入为-100，那么softmax层的对于该输入的输出为0，即使增加了10，由-100变成了-90，仍然为0，显然这对输出没有什么影响。而如果softmax层最大的输入为10，将其更改为了0，显然这会使得输出产生巨大的变化。而JSMA的攻击方式并不会考虑从0到10和从-100到-90的不同，他是一视同仁的。
 而在蒸馏训练之后，会使得这样的不同放大。假设输出类向量为：[ -674.3225 , -371.59705 , -177.78831 , 562.87225 ,-1313.5781 , 998.18207 , -886.97107 , -511.58194 ,-126.719666, -43.129272]。要改变类别实际上只需要第四个数比第六个数大即可（即562增长，998下降）。但是JSMA会由于增长562会使得例如-1313,-886的数增加很多而放弃。这实际上是算法本身的问题。
 要攻击防御性蒸馏模型实际上很简单，只需要不考虑这些其他的类向量值，只考虑需要超过的类向量和自身的类向量值即可，甚至可以只关注增加自身的类向量。
 因此作者Nicholas Carlini和David Wagner提出了一系列能够改变类向量的目标函数：

\begin{equation}\nonumber \begin{aligned} f_1(x') &= -loss_{F,t}(x')+1 \\ f_2(x') &= (max_{i \neq t} (F(x')_i) - F(x')_t)^+ \\ f_3(x') &= softplus(max_{i \neq t} (F(x')_i) - F(x')_t) -log(2) \\ f_4(x') &= (0.5 - F(x')_t)^+ \\ f_5(x') &= -\log(2F(x')_t -2) \\ f_6(x') &= (max_{i \neq t} (Z(x')_i) - Z(x')_t)^+ \\ f_7(x') &= softplus(max_{i \neq t}Z(x')_i) - Z(x')_t) - log(2) \end{aligned} \end{equation}