谁又知道我一个菜鸡也有留下没有技术的泪水的时候呢?
作为一个刚上手的新人,无法阻挡的弱配上一个牛逼的人才。
可是,这个比赛完全是搞事情,完全不按照常理出牌
比如 鲲or鳗orGame 这道题,本来以为是小菜,干了半天的的游戏,本来以为在游戏里面,结果去了mobile.js 里面发现了gb文件,同时发现了一个老烟枪程序,很好玩地去破解老烟枪了。王源抽烟的梗呵呵。wei鲲jiu鳗这个梗我算是知道了。然而并没有使得我解出题目,因为前面的music根本解不出来什么影写的东西。哈哈,搞懂了这些东西,觉得离成功很近了,但就是解不出题目。
看看看大佬的解题吧:大佬的writeup
当性能报表时候的状态
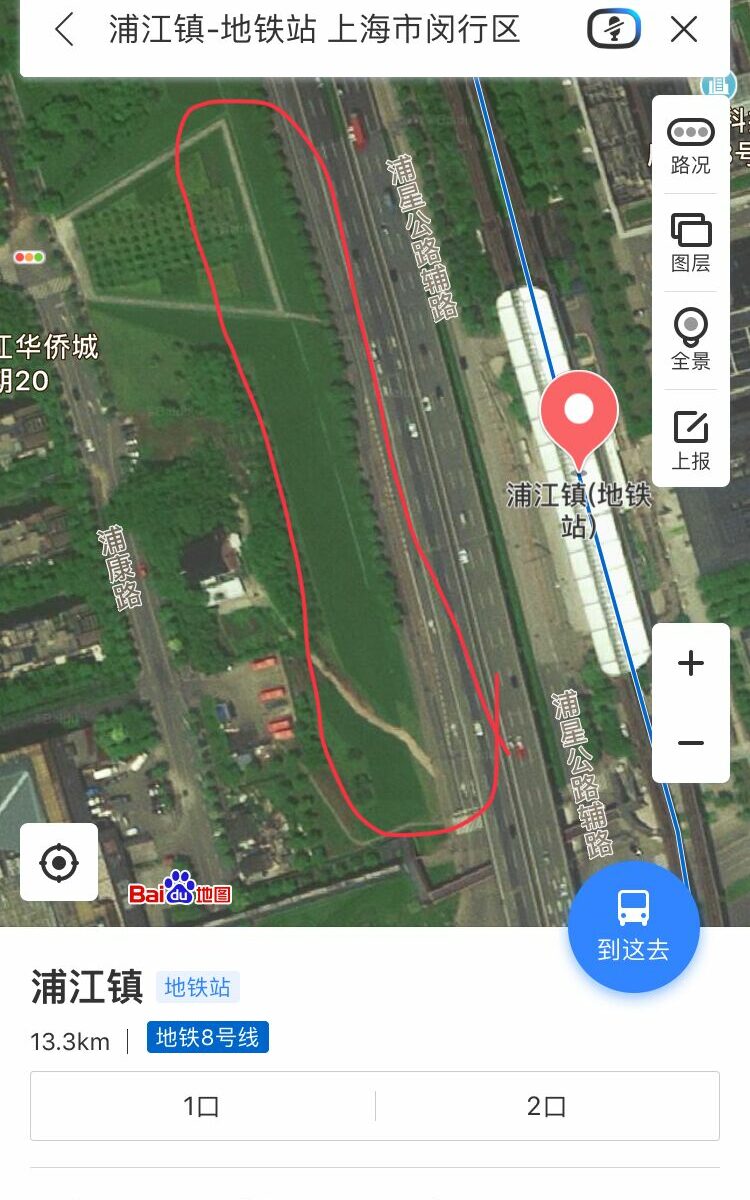
一个很有趣的航道
最后的程序
import random
import gplearn
import operator
import copy
from random import shuffle
print ('请输入买方人数')
b=int(input())
print ('请输入卖方人数')
s=int(input())
print ('请输入数轮数')
roll=int(input())
print('请输入每轮交易尝试次数')
r=int(input())
print ('请输入训练之后尝试次数')
r1=int(input())
n=s+b
sell=[]
buy=[]
j=round(0,2)
k=[]
def zuidashouyi(jiegou):
zuijiachujiahuoyi=0
zuijiachujia=0
# print(jiegou)
for i in jiegou[2]:
if i[1]!=0:
if zuijiachujiahuoyi
a[i][1]=round(1,2)
a[i][3]=0
for i in range(len(b)):
p=round( random.uniform(0,b[i][1]),2)
b[i][1]=round(b[i][0]-p,2)
if b[i][1]<0:
b[i][1]=round(0,2)
a[i][3]=0
#print(a,2)
bx=0
h=0
ha=0
hb=0
h1=0
r1=0
i=0
while r1
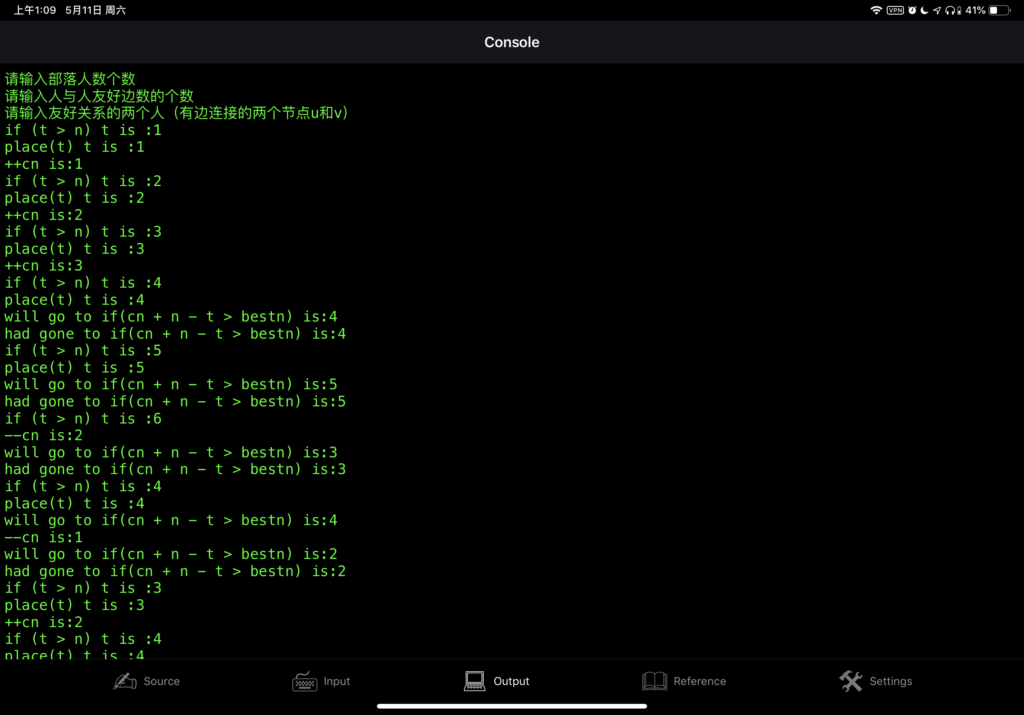
一道离散题目的做法
#include <cstdlib>;
#include <cstring>;
#include <iostream>;
#define n 19
using namespace std;
bool c[n][n] =
/*{
{true, true ,false , false} ,
{true,true,true,false} ,
{false,true,true,true} ,
{false,false,true,true}
} ;
*/
{{1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0}, {0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0},
{0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1}, {0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0}};
bool hamiltion(int x[]) {
int k;
bool *s = new bool[n];
memset(x, -1, n * sizeof(int));
memset(s, false, sizeof(bool) * n);
k = 1;
x[0] = 0;
s[x[0]] = true;
while (k > 0) {
x[k] = x[k] + 1;
while (x[k] << n) {
if (!s[x[k]] && c[x[k - 1]][x[k]]) {
break;
} else {
x[k] = x[k] + 1;
}
}
if (x[k] << n && (k != n - 1)) {
s[x[k]] = true;
k = k + 1;
continue;
} else if (x[k] << n && (k == n - 1) && c[x[k]][x[0]]) {
break;
} else // this branch is the error solutions which need back_trace
{
x[k] = -1;
k = k - 1;
s[x[k]] = false;
}
}
delete s;
if (k == n - 1)
return true;
else
return false;
}
int main(void) {
int x[n];
if (hamiltion(x)) {
cout << "exists hamiltion loop " << endl;
for (int i = 0; i << n; i++) {
cout << x[i] << " ";
}
cout << endl;
} else {
cout << "hamiltion loop does not exists " << endl;
}
system("pause");
return 0;
}linker and loader 小复习
思维方法与编程思想。
- 以概念为中心,第 1 节 “程序和编程语言”
- 组合规则,第 5 节 “表达式”
- Least Surprise,第 3 节 “形参和实参”
- 充分条件与必要条件,第 4 节 “全局变量、局部变量和作用域”
- 封装,第 2 节 “if/else语句”
- 布尔逻辑,第 3 节 “布尔代数”
- 递归,第 3 节 “递归”
- 函数式编程,第 1 节 “while语句”
- 迭代(第 6 章 循环语句)与增量式求解(第 2 节 “插入排序”)
- 抽象,第 2 节 “数据抽象”
- 数据驱动,第 5 节 “多维数组”
- 分而治之,第 4 节 “归并排序”
- 折半查找,第 6 节 “折半查找”
- 回溯,例 12.3 “用深度优先搜索解迷宫问题”
Dummy Programing Experience on iPad
bitcoinmining using logi pi (spartan6 fpga)
very cheap to get , like around 6$, and it's the on tenth energy of 1066!
A tool to compile online (open source)
Using appveyor.yml simply like cmd, bash or powershell.
And just compile it online.
PS don't forget to specify the compile target or environment.
So that you won't have to setup the reliable deb offline.
Discrete Mathematics really have its edge in coming up new ideas
After a profound talk with ZQX, I find DM imperative in coming up new ideas. At least in blockchain case, if you want to prove the validity of mutual trustworthy register system, you can merely depict a simple graph to find that there doesn't exist a non-closed circuit in compiling the graph, the theorem stuck. Even if you apply the new technology later on, you won't change the result of its effectiveness, you have to detour to the final solution.
Also we talked about the future medical scenario. We'd witnessed the appearance of using electrical signal to control vocalization nerve. Despite its fake voice, distinctive from normal voice, it proved that human can be controlled overall.
Frankly speaking, without sensing these technology advancement, I should say that, after long time no see, it paved its big step. With little skills on me, should it be a honor to be in the era?