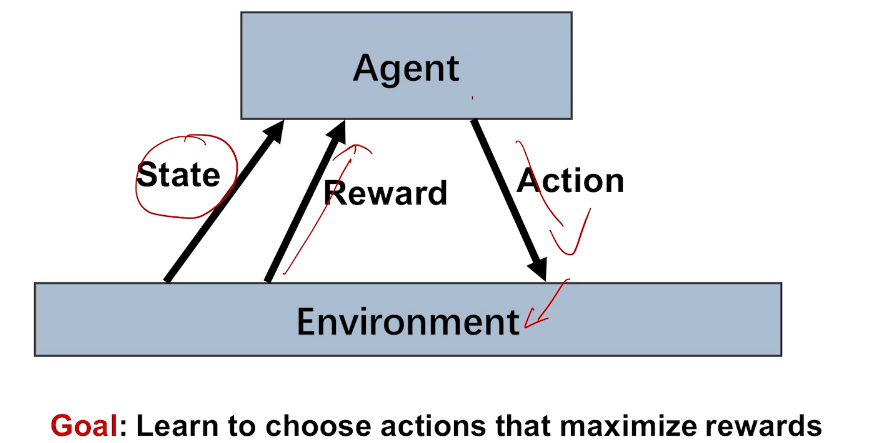
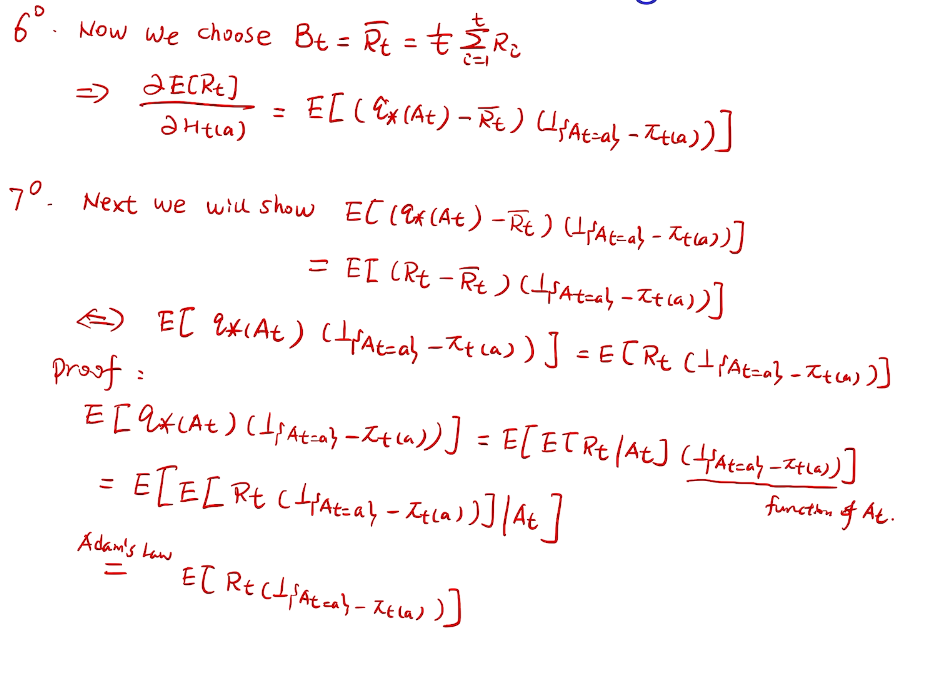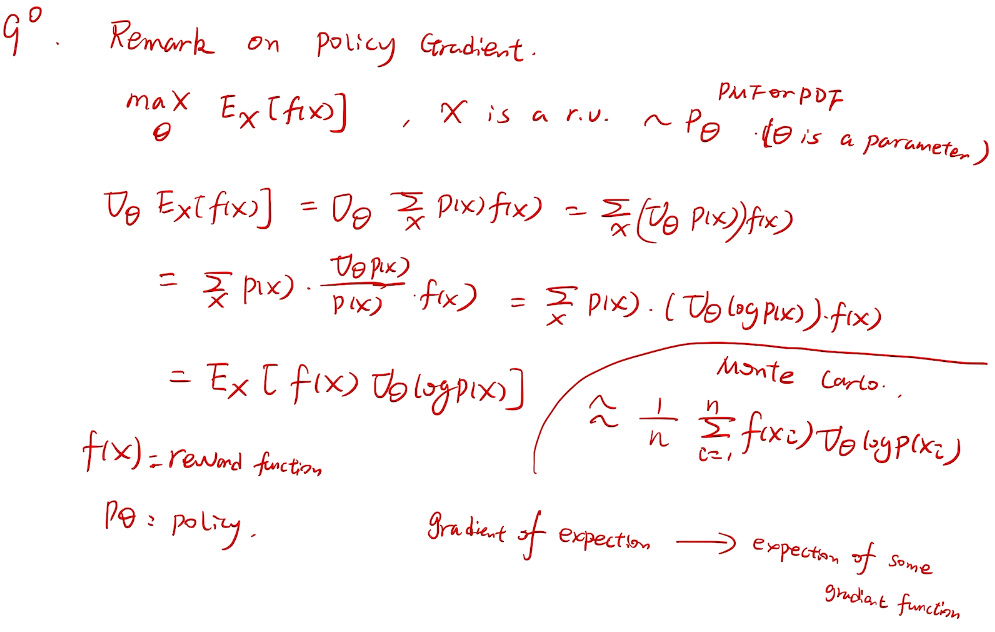反馈:奖励
agent
action
bandit 是强化学习的特例
利用与探索的两难

短期与长期的对决
现实中的例子

两臂老虎机
三种类型

奖励模型

Decision making under uncertainty
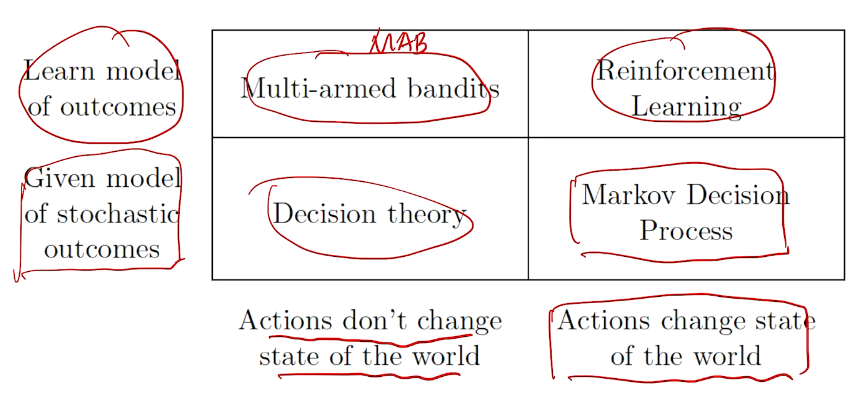
action vs. reward

types of reward

types of rewards model

types of context

example

先验or后验
structured
global
summary

example
网飞 展示广告
随机bandit

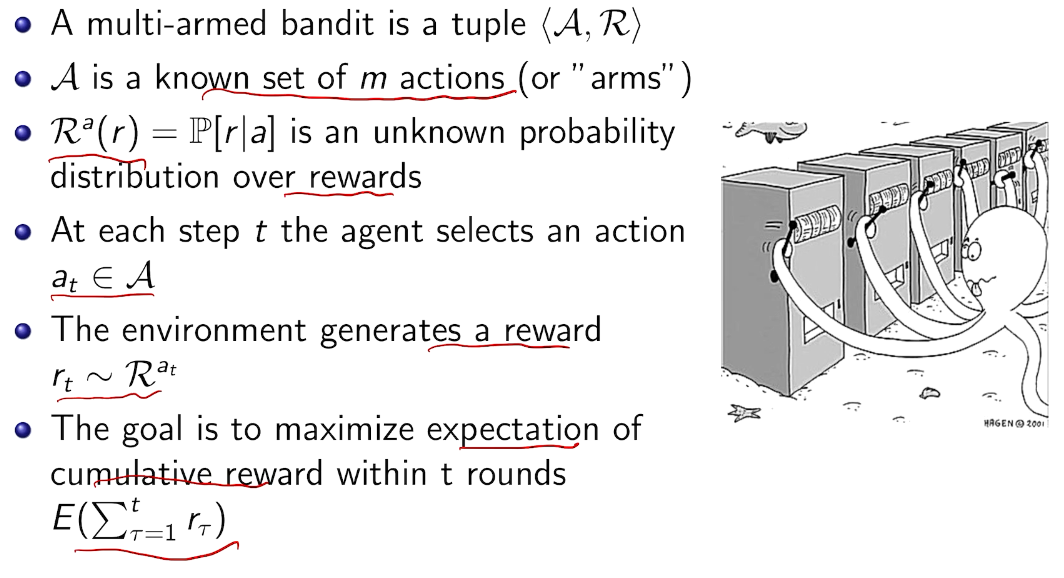
regret: equivalent goal
the value of an arbitrary action a is the mean reward for a (unknown):
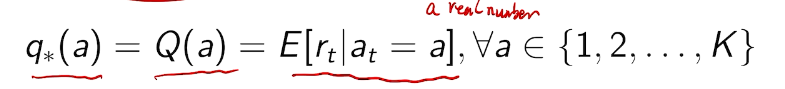
the optimal value is 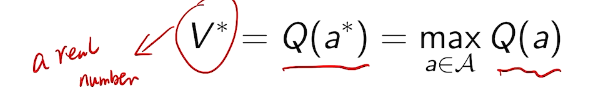
we care about total regret
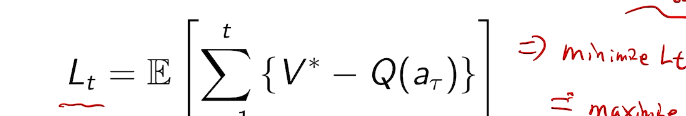
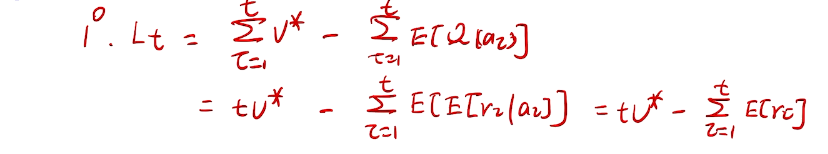
example on a
In general, those values are unknown.
we must try actions to learn the action-values(explore), and prefer those that appear best(exploit).

action-value methods
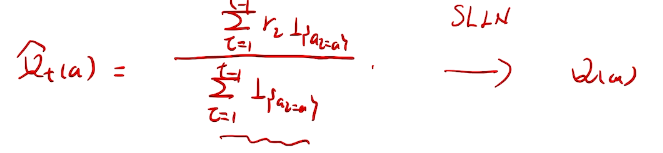
methods that learn action-value estimates and nothing else
根据强大数定理。收敛于真实期望值。
counting regret

桥梁:计算total regret。 变量为指示变量

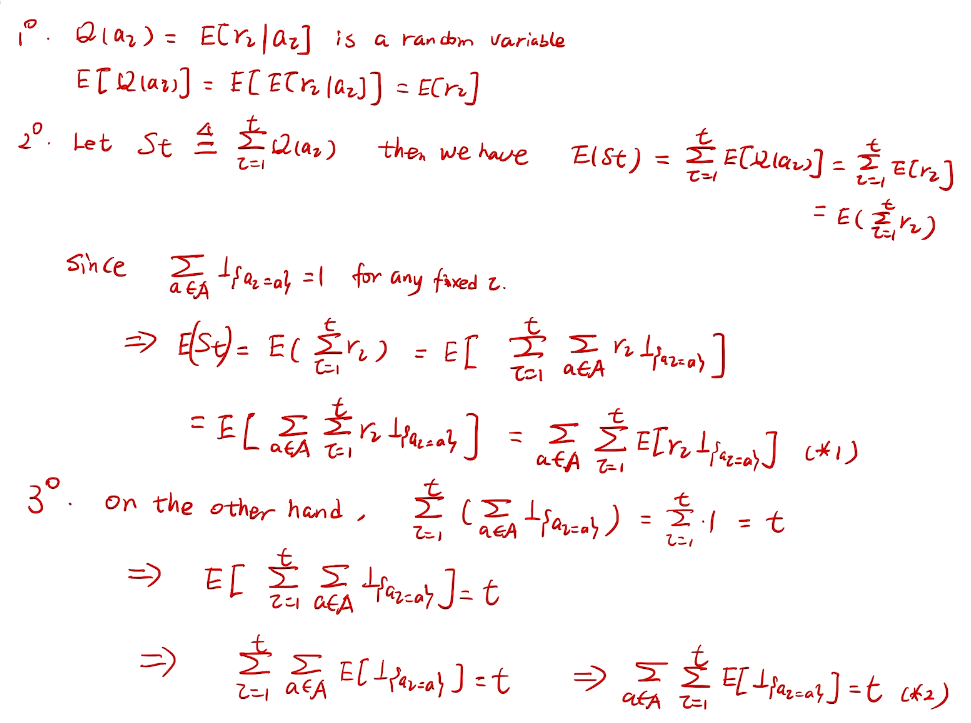
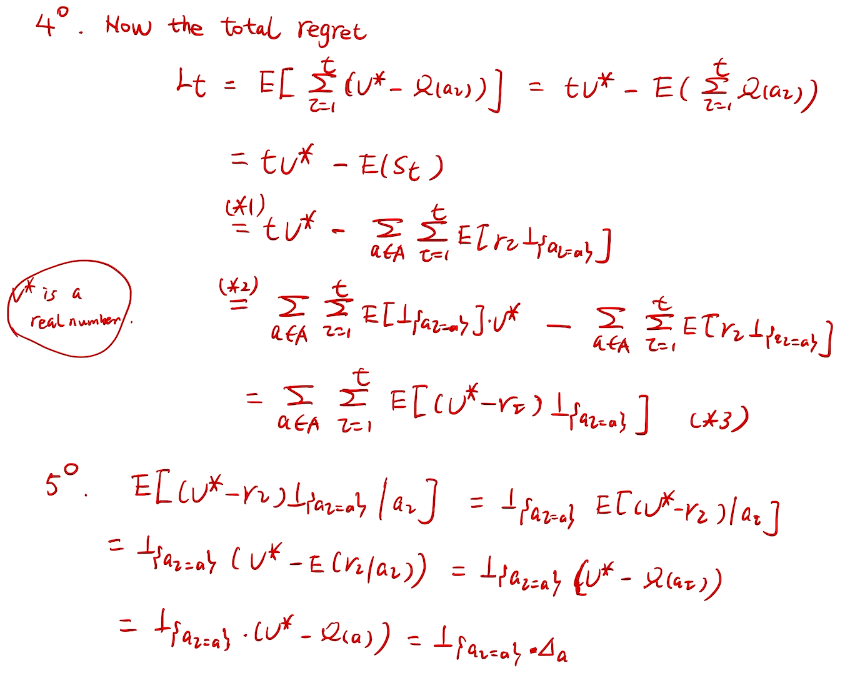
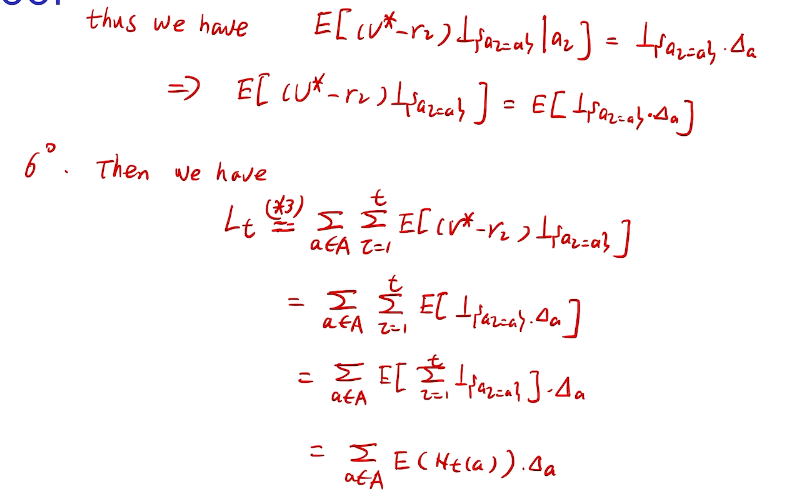
亚当定理:得到lemma的结果
how to define a good learner.
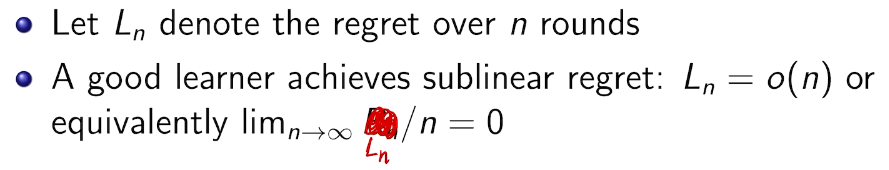
linear!! 有两种情况

Greedy algorithm

每次取最高的期望
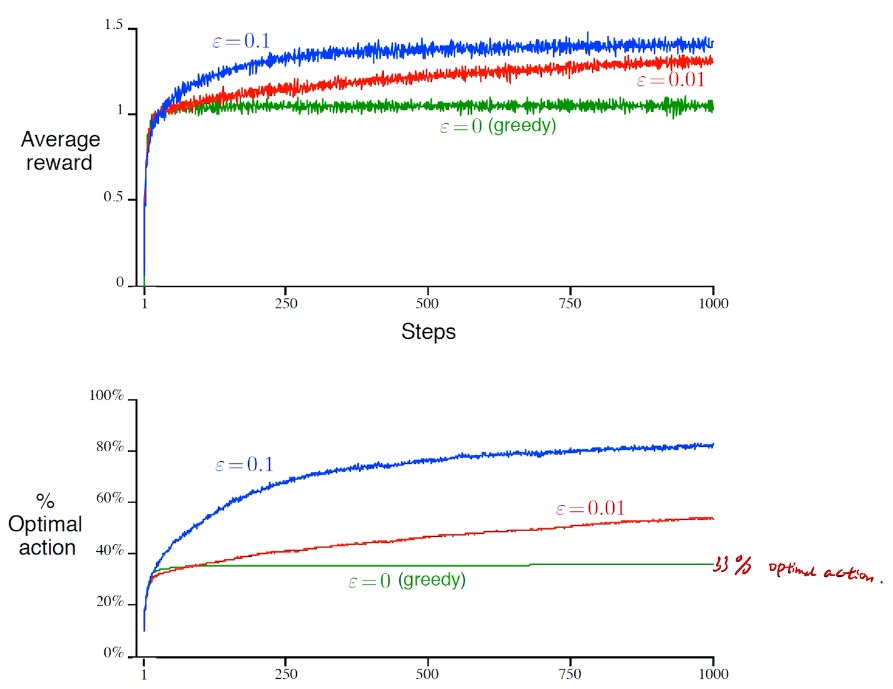
\(\epsilon - greedy\)
防止出现局部最优

proof of lower bound
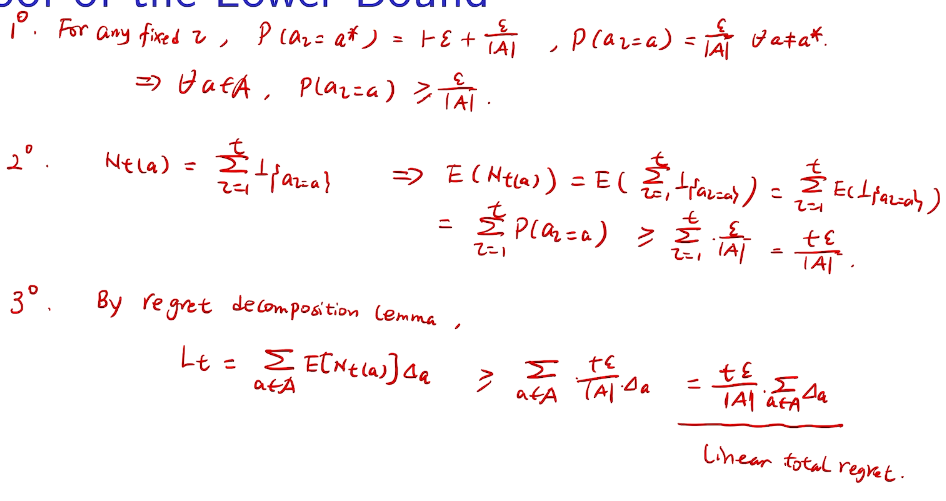
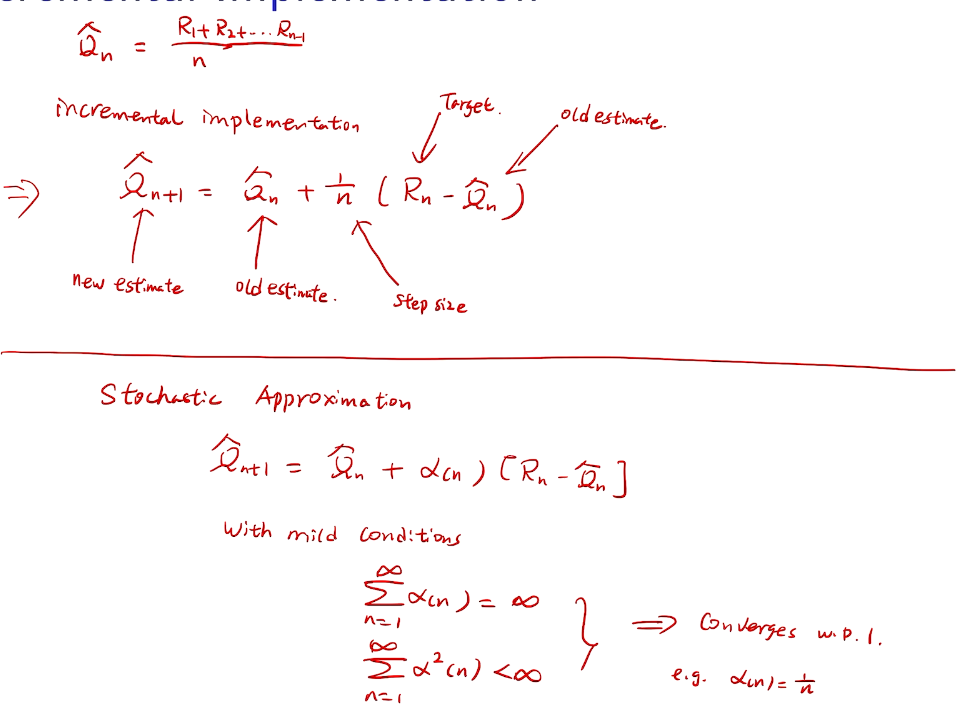
incremental implementation
性能考量、实现在线学习
proof
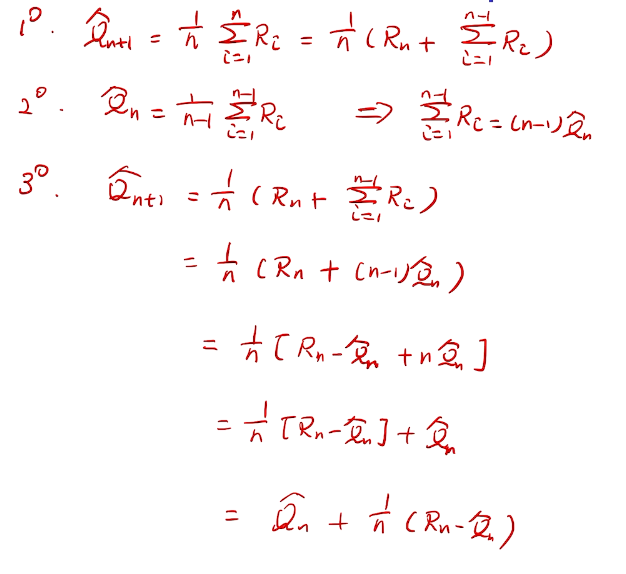
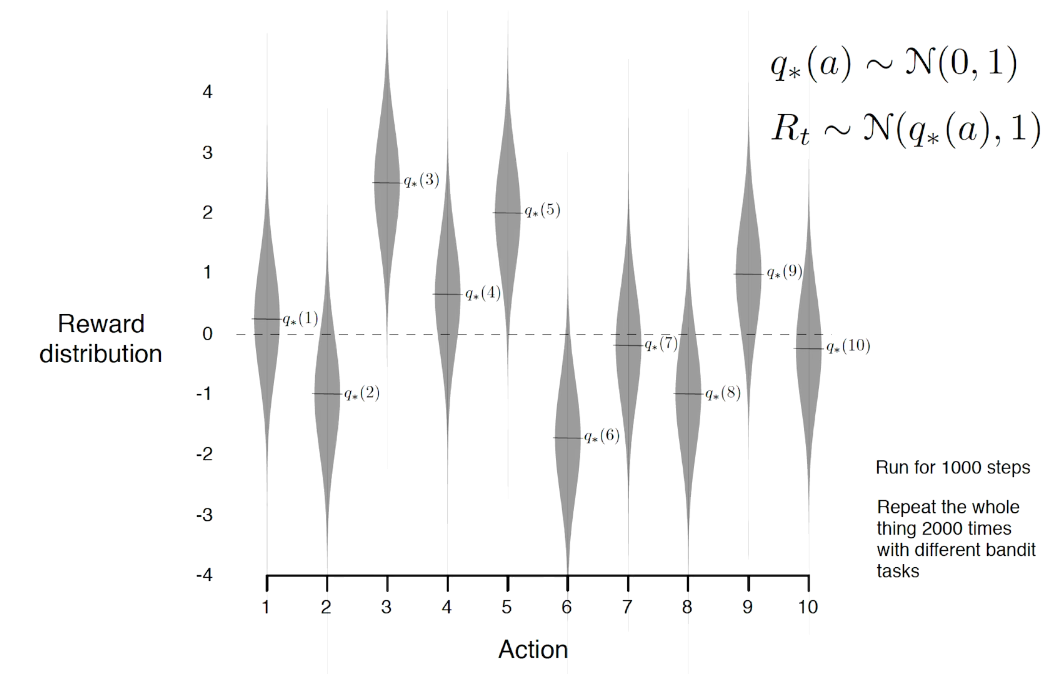
bandit notation

进一步提高性能 Optimistic Initial values
All methods s ofar depends on 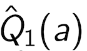 which is 0 in this case. but we can do 5.
which is 0 in this case. but we can do 5.
Initally bad case for more 尝试。
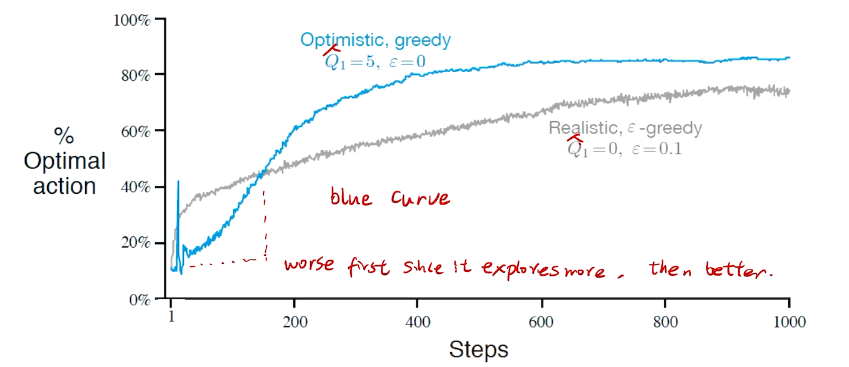
algorithm

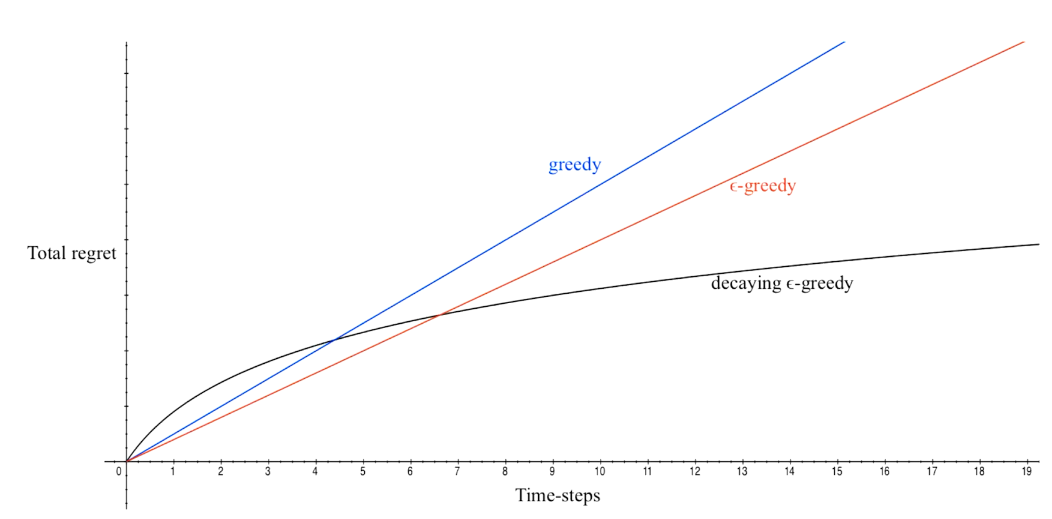
DecayIng \(\epsilon _{t} -Greedy\)
insight:先降后升

 ## bandit algorithm lower bounds(depends on gaps)
## bandit algorithm lower bounds(depends on gaps)

Optimism in the face of uncertainty
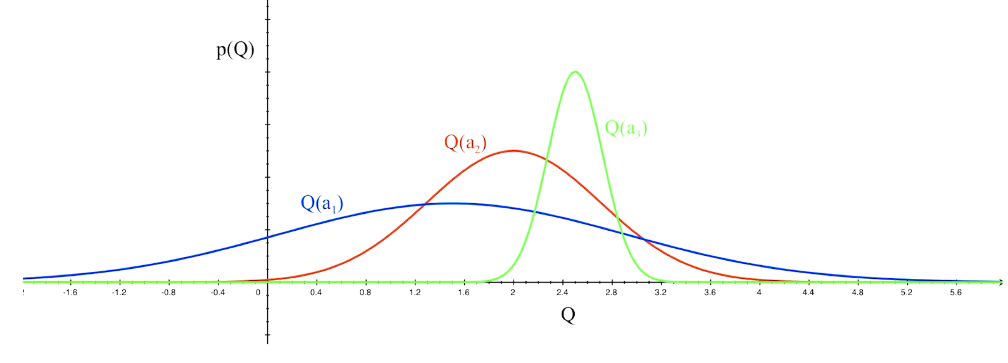
which action to pick?

越未知需要探索
Upper Confidence Bound

hoeffding's inequality

general case

calculation

取bound得到置信区间的位置
UCB1

action 没有被充分的探索过,所以需要探索
上界探索
credit:https://jeremykun.com/2013/10/28/optimism-in-the-face-of-uncertainty-the-ucb1-algorithm/
Theorem: Suppose UCB1 is run as above. Then its expected cumulative regret 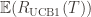 is at most$\displaystyle 8 \sum_{i : \mu_i < \mu^*} \frac{\log T}{\Delta_i} + \left ( 1 + \frac{\pi^2}{3} \right ) \left ( \sum_{j=1}^K \Delta_j \right )$
is at most$\displaystyle 8 \sum_{i : \mu_i < \mu^*} \frac{\log T}{\Delta_i} + \left ( 1 + \frac{\pi^2}{3} \right ) \left ( \sum_{j=1}^K \Delta_j \right )$
Okay, this looks like one nasty puppy, but it’s actually not that bad. The first term of the sum signifies that we expect to play any suboptimal machine about a logarithmic number of times, roughly scaled by how hard it is to distinguish from the optimal machine. That is, if 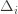 is small we will require more tries to know that action
is small we will require more tries to know that action 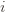 is suboptimal, and hence we will incur more regret. The second term represents a small constant number (the $1 + \pi^2 / 3$ part) that caps the number of times we’ll play suboptimal machines in excess of the first term due to unlikely events occurring. So the first term is like our expected losses, and the second is our risk.
is suboptimal, and hence we will incur more regret. The second term represents a small constant number (the $1 + \pi^2 / 3$ part) that caps the number of times we’ll play suboptimal machines in excess of the first term due to unlikely events occurring. So the first term is like our expected losses, and the second is our risk.
But note that this is a worst-case bound on the regret. We’re not saying we will achieve this much regret, or anywhere near it, but that UCB1 simply cannot do worse than this. Our hope is that in practice UCB1 performs much better.
Before we prove the theorem, let’s see how derive the 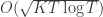 bound mentioned above. This will require familiarity with multivariable calculus, but such things must be endured like ripping off a band-aid. First consider the regret as a function
bound mentioned above. This will require familiarity with multivariable calculus, but such things must be endured like ripping off a band-aid. First consider the regret as a function  (excluding of course
(excluding of course 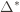 ), and let’s look at the worst case bound by maximizing it. In particular, we’re just finding the problem with the parameters which screw our bound as badly as possible, The gradient of the regret function is given by
), and let’s look at the worst case bound by maximizing it. In particular, we’re just finding the problem with the parameters which screw our bound as badly as possible, The gradient of the regret function is given by
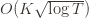
and it’s zero if and only if for each 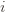 ,
, 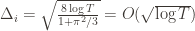 . However this is a minimum of the regret bound (the Hessian is diagonal and all its eigenvalues are positive). Plugging in the
. However this is a minimum of the regret bound (the Hessian is diagonal and all its eigenvalues are positive). Plugging in the 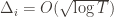 (which are all the same) gives a total bound of
(which are all the same) gives a total bound of 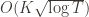 . If we look at the only possible endpoint (the
. If we look at the only possible endpoint (the 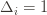 ), then we get a local maximum of
), then we get a local maximum of 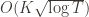 . But this isn’t the
. But this isn’t the 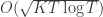 we promised, what gives? Well, this upper bound grows arbitrarily large as the
we promised, what gives? Well, this upper bound grows arbitrarily large as the 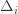 go to zero. But at the same time, if all the
go to zero. But at the same time, if all the 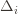 are small, then we shouldn’t be incurring much regret because we’ll be picking actions that are close to optimal!
are small, then we shouldn’t be incurring much regret because we’ll be picking actions that are close to optimal!
Indeed, if we assume for simplicity that all the 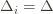 are the same, then another trivial regret bound is
are the same, then another trivial regret bound is 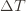 (why?). The true regret is hence the minimum of this regret bound and the UCB1 regret bound: as the UCB1 bound degrades we will eventually switch to the simpler bound. That will be a non-differentiable switch (and hence a critical point) and it occurs at
(why?). The true regret is hence the minimum of this regret bound and the UCB1 regret bound: as the UCB1 bound degrades we will eventually switch to the simpler bound. That will be a non-differentiable switch (and hence a critical point) and it occurs at 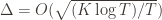 . Hence the regret bound at the switch is
. Hence the regret bound at the switch is 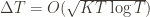 , as desired.
, as desired.
Proving the Worst-Case Regret Bound
Proof. The proof works by finding a bound on  , the expected number of times UCB chooses an action up to round
, the expected number of times UCB chooses an action up to round 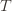 . Using the
. Using the 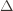 notation, the regret is then just
notation, the regret is then just 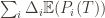 , and bounding the
, and bounding the 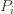 ‘s will bound the regret.
‘s will bound the regret.
Recall the notation for our upper bound  and let’s loosen it a bit to
and let’s loosen it a bit to 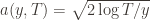 so that we’re allowed to “pretend” a action has been played
so that we’re allowed to “pretend” a action has been played 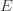 times. Recall further that the random variable
times. Recall further that the random variable 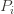 has as its value the index of the machine chosen. We denote by
has as its value the index of the machine chosen. We denote by  the indicator random variable for the event
the indicator random variable for the event 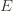 . And remember that we use an asterisk to denote a quantity associated with the optimal action (e.g.,
. And remember that we use an asterisk to denote a quantity associated with the optimal action (e.g., 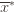 is the empirical mean of the optimal action).
is the empirical mean of the optimal action).
Indeed for any action 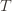 , the only way we know how to write down
, the only way we know how to write down  is as
is as

The 1 is from the initialization where we play each action once, and the sum is the trivial thing where just count the number of rounds in which we pick action 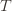 . Now we’re just going to pull some number
. Now we’re just going to pull some number 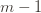 of plays out of that summation, keep it variable, and try to optimize over it. Since we might play the action fewer than
of plays out of that summation, keep it variable, and try to optimize over it. Since we might play the action fewer than 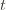 times overall, this requires an inequality.
times overall, this requires an inequality.

These indicator functions should be read as sentences: we’re just saying that we’re picking action 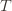 in round
in round 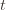 and we’ve already played
and we’ve already played 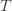 at least
at least 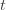 times. Now we’re going to focus on the inside of the summation, and come up with an event that happens at least as frequently as this one to get an upper bound. Specifically, saying that we’ve picked action
times. Now we’re going to focus on the inside of the summation, and come up with an event that happens at least as frequently as this one to get an upper bound. Specifically, saying that we’ve picked action 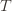 in round
in round 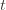 means that the upper bound for action
means that the upper bound for action 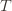 exceeds the upper bound for every other action. In particular, this means its upper bound exceeds the upper bound of the best action (and
exceeds the upper bound for every other action. In particular, this means its upper bound exceeds the upper bound of the best action (and 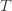 might coincide with the best action, but that’s fine). In notation this event is
might coincide with the best action, but that’s fine). In notation this event is
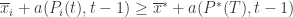
Denote the upper bound  for action
for action 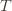 in round
in round 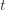 by
by  . Since this event must occur every time we pick action
. Since this event must occur every time we pick action 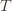 (though not necessarily vice versa), we have
(though not necessarily vice versa), we have

We’ll do this process again but with a slightly more complicated event. If the upper bound of action 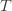 exceeds that of the optimal machine, it is also the case that the maximum upper bound for action
exceeds that of the optimal machine, it is also the case that the maximum upper bound for action 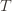 we’ve seen after the first
we’ve seen after the first 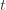 trials exceeds the minimum upper bound we’ve seen on the optimal machine (ever). But on round
trials exceeds the minimum upper bound we’ve seen on the optimal machine (ever). But on round 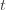 we don’t know how many times we’ve played the optimal machine, nor do we even know how many times we’ve played machine
we don’t know how many times we’ve played the optimal machine, nor do we even know how many times we’ve played machine 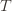 (except that it’s more than
(except that it’s more than 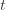 ). So we try all possibilities and look at minima and maxima. This is a pretty crude approximation, but it will allow us to write things in a nicer form.
). So we try all possibilities and look at minima and maxima. This is a pretty crude approximation, but it will allow us to write things in a nicer form.
Denote by 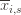 the random variable for the empirical mean after playing action
the random variable for the empirical mean after playing action 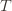 a total of
a total of  times, and
times, and 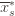 the corresponding quantity for the optimal machine. Realizing everything in notation, the above argument proves that
the corresponding quantity for the optimal machine. Realizing everything in notation, the above argument proves that

Indeed, at each  for which the max is greater than the min, there will be at least one pair
for which the max is greater than the min, there will be at least one pair  for which the values of the quantities inside the max/min will satisfy the inequality. And so, even worse, we can just count the number of pairs
for which the values of the quantities inside the max/min will satisfy the inequality. And so, even worse, we can just count the number of pairs  for which it happens. That is, we can expand the event above into the double sum which is at least as large:
for which it happens. That is, we can expand the event above into the double sum which is at least as large:
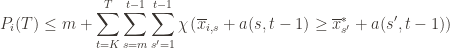
We can make one other odd inequality by increasing the sum to go from 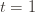 to
to 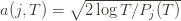 . This will become clear later, but it means we can replace
. This will become clear later, but it means we can replace 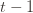 with
with 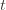 and thus have
and thus have

Now that we’ve slogged through this mess of inequalities, we can actually get to the heart of the argument. Suppose that this event actually happens, that 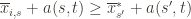 . Then what can we say? Well, consider the following three events:
. Then what can we say? Well, consider the following three events:
(1) 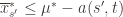
(2) 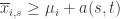
(3) 
In words, (1) is the event that the empirical mean of the optimal action is less than the lower confidence bound. By our Chernoff bound argument earlier, this happens with probability 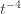 . Likewise, (2) is the event that the empirical mean payoff of action
. Likewise, (2) is the event that the empirical mean payoff of action 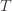 is larger than the upper confidence bound, which also occurs with probability
is larger than the upper confidence bound, which also occurs with probability 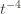 . We will see momentarily that (3) is impossible for a well-chosen
. We will see momentarily that (3) is impossible for a well-chosen 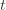 (which is why we left it variable), but in any case the claim is that one of these three events must occur. For if they are all false, we have
(which is why we left it variable), but in any case the claim is that one of these three events must occur. For if they are all false, we have
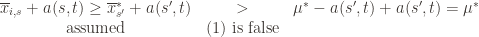
and

But putting these two inequalities together gives us precisely that (3) is true:

This proves the claim.
By the union bound, the probability that at least one of these events happens is 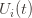 plus whatever the probability of (3) being true is. But as we said, we’ll pick
plus whatever the probability of (3) being true is. But as we said, we’ll pick 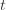 to make (3) always false. Indeed
to make (3) always false. Indeed 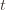 depends on which action
depends on which action 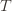 is being played, and if
is being played, and if 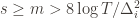 then
then 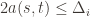 , and by the definition of
, and by the definition of 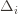 we have
we have
 .
.
Now we can finally piece everything together. The expected value of an event is just its probability of occurring, and so
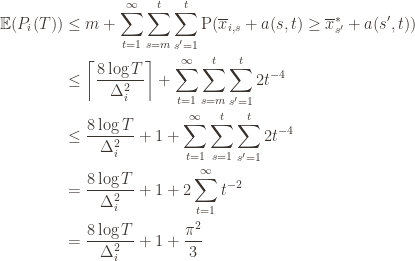
The second line is the Chernoff bound we argued above, the third and fourth lines are relatively obvious algebraic manipulations, and the last equality uses the classic solution to Basel’s problem. Plugging this upper bound in to the regret formula we gave in the first paragraph of the proof establishes the bound and proves the theorem.
result
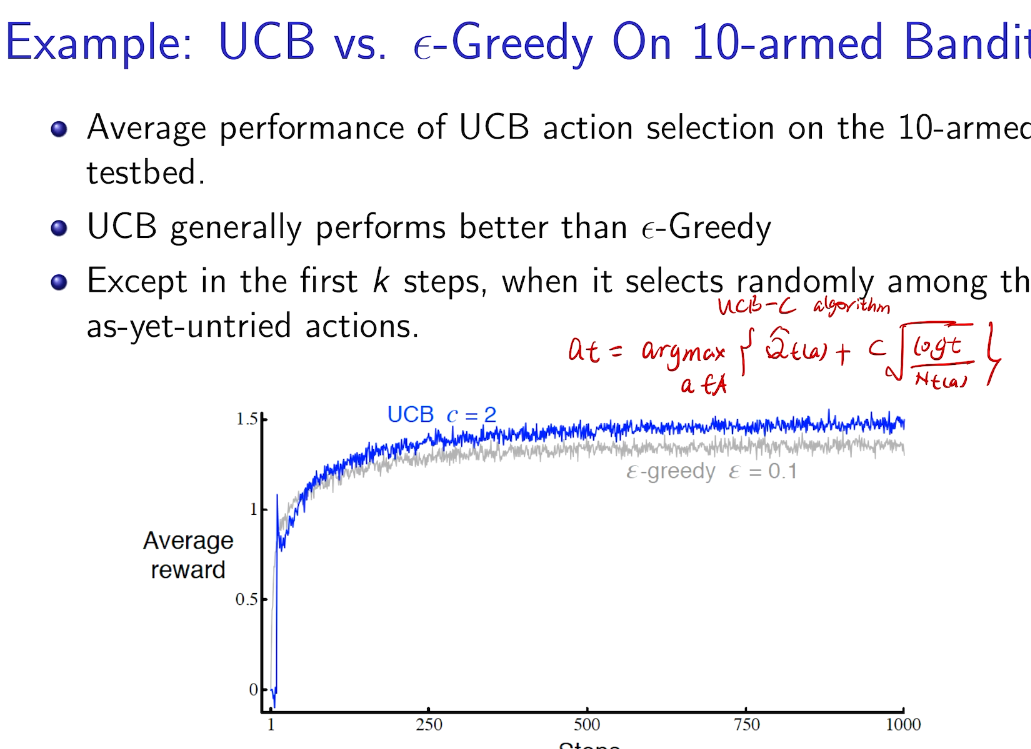
Intro for Thompson Sampling
Probability Matching

~ 最大后验概率

history

在知道后验的情况下比UCB 好
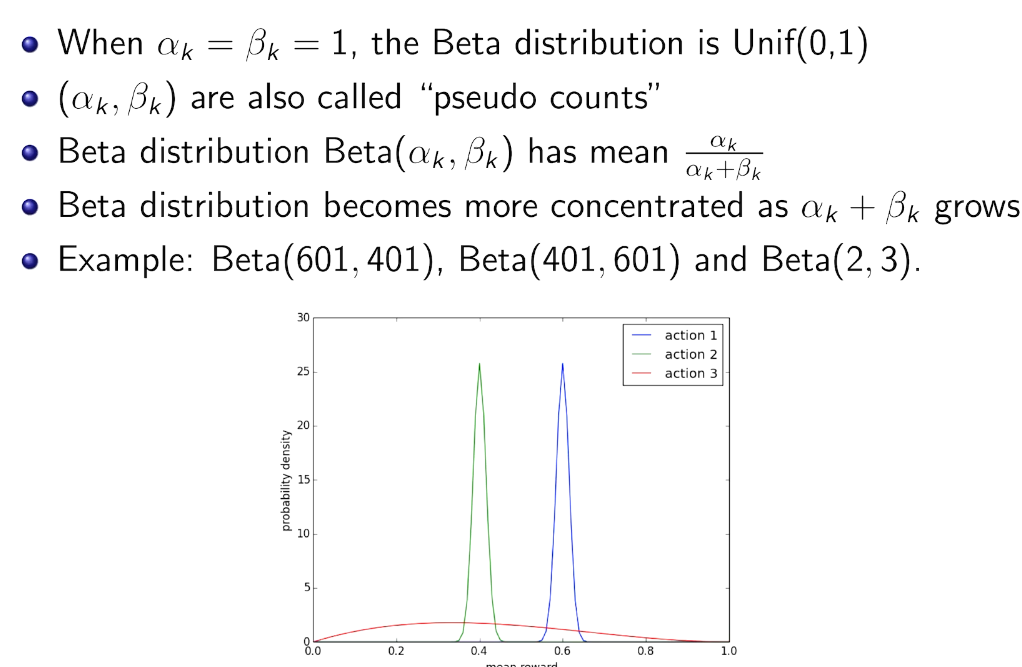
beta-bernoulli bandit

先验共轭
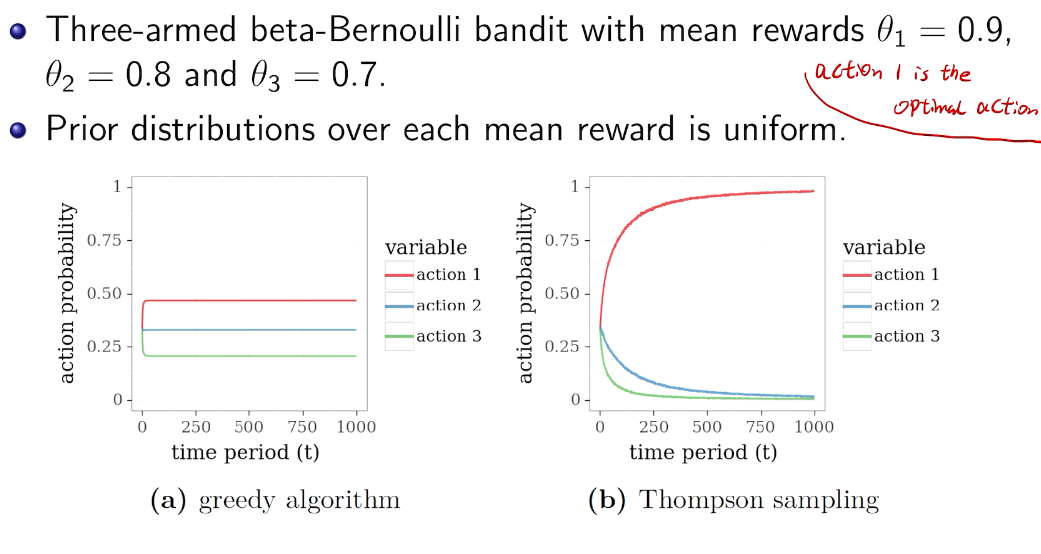
greedy vs. Thompson Sampling

第一步不一样。 期望 vs 样本值
simulation
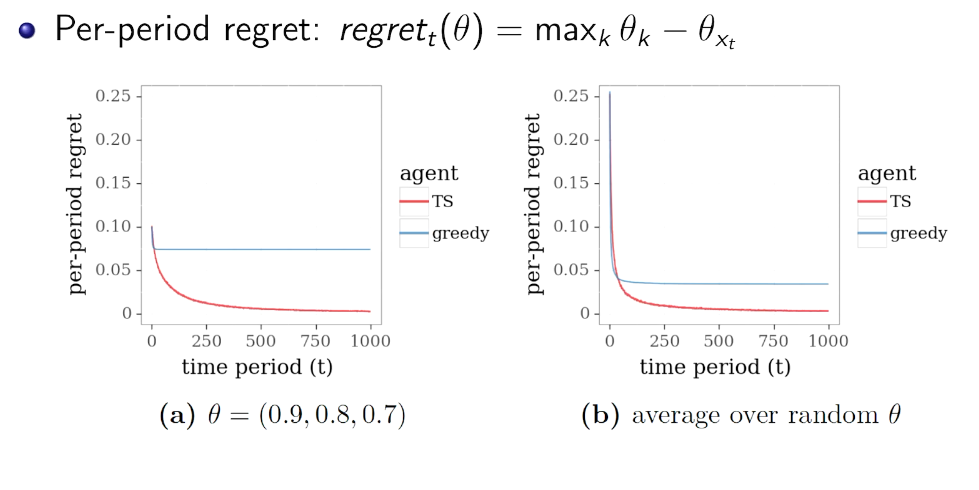
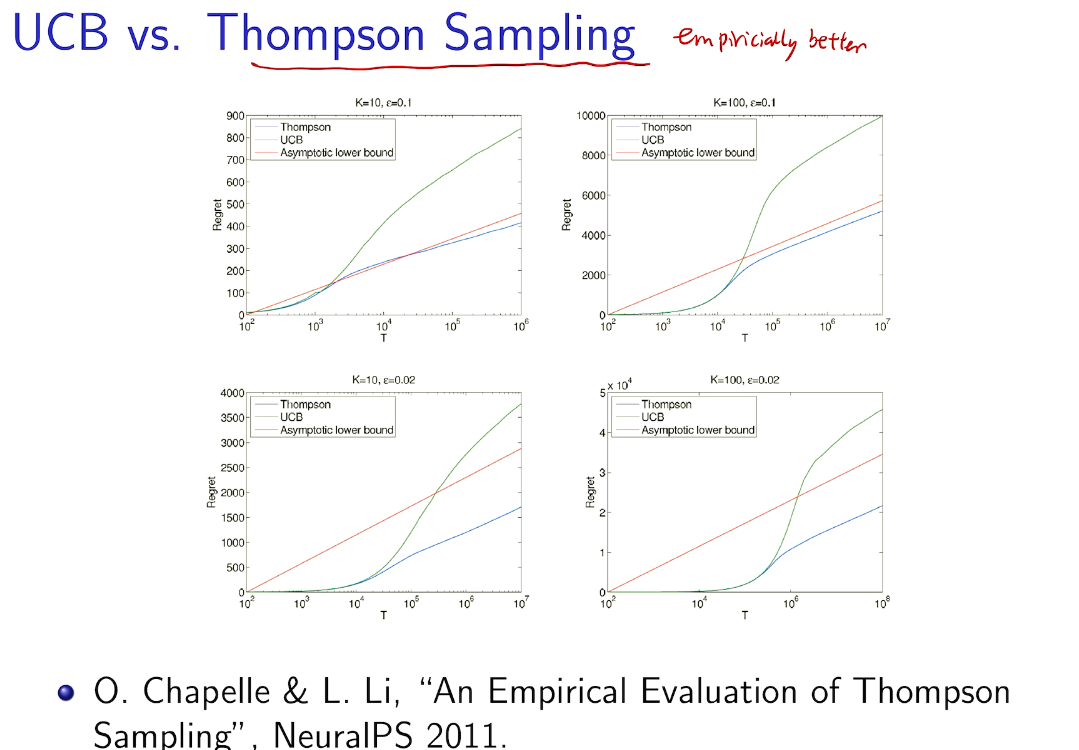
Other kind of Bayesian inference

梯度bandit 算法
随机梯度上升法
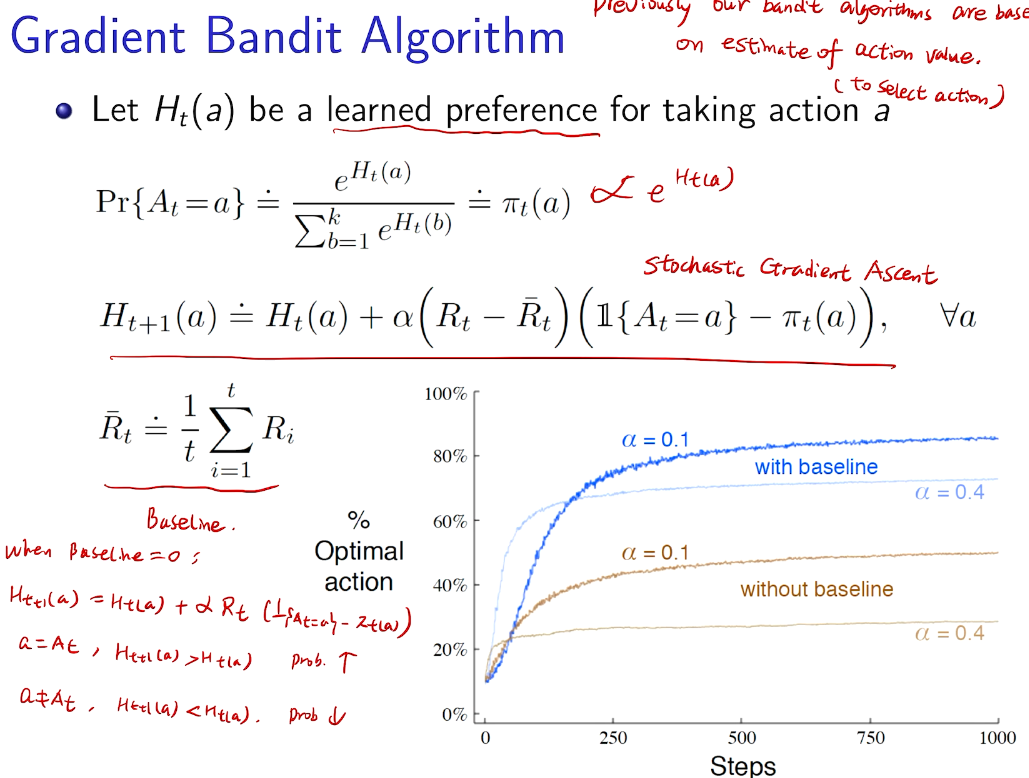
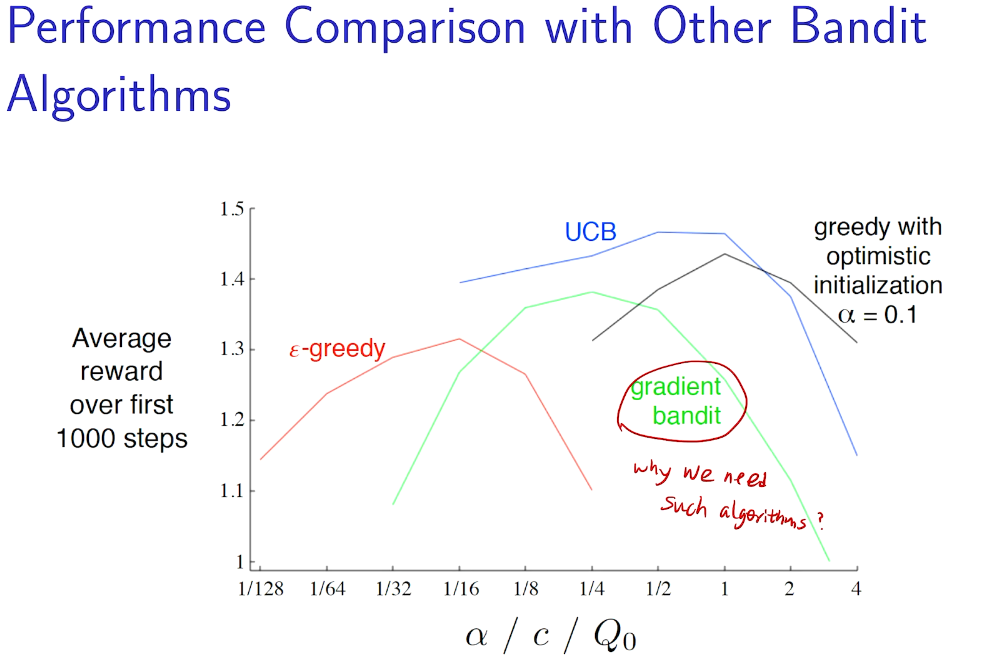
why not 梯度下降?
more general for RL

proof


// lemma 1 for homework

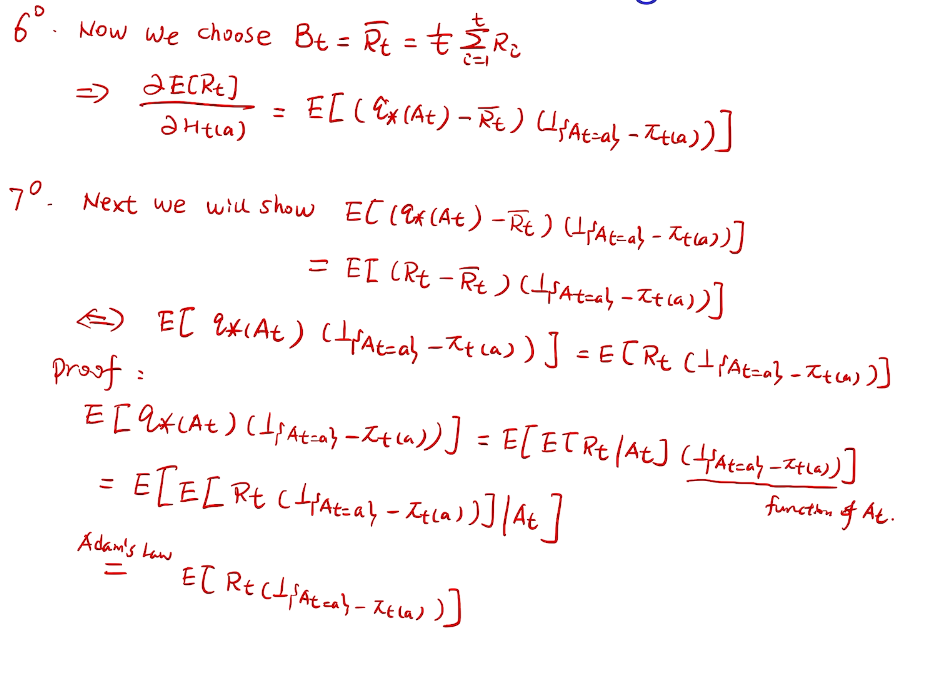

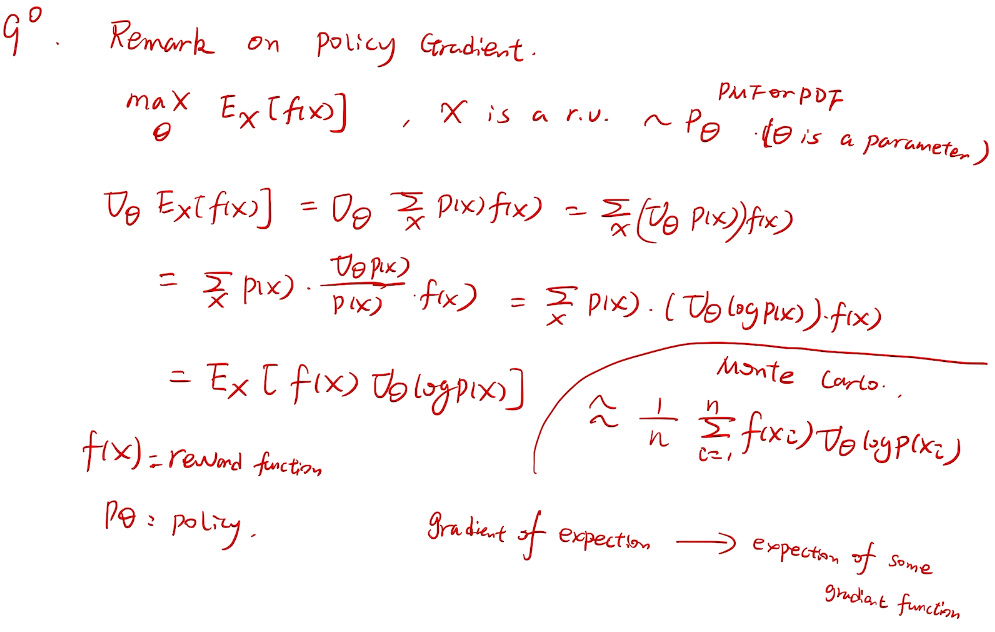
梯度的期望->期望的梯度
Adversarial Bandit

simple bandit game


importance-weighted estimators

用于估计其他未被触发的arm
another good algorithm

bias ~ variance tradeoff
方差太大。
几率小的reward 现在增大了。 用隐含的增加的探索来使反差减少
algorithm

adversary bandits with expert's advice


意见的权重的分布=》exp4
additional exploration
uniform exploration
proved no need

summary

bound
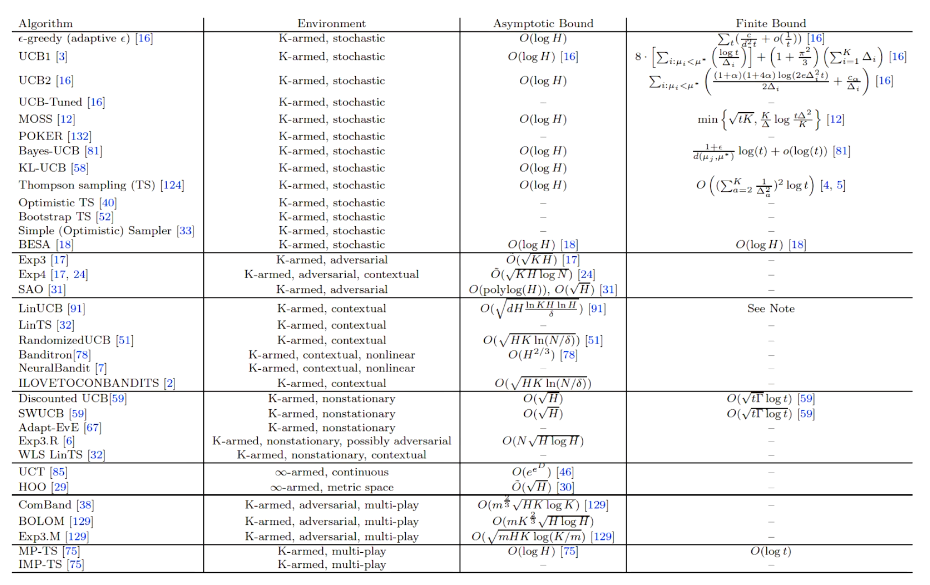
看作为独立为RL之外的眼界方向





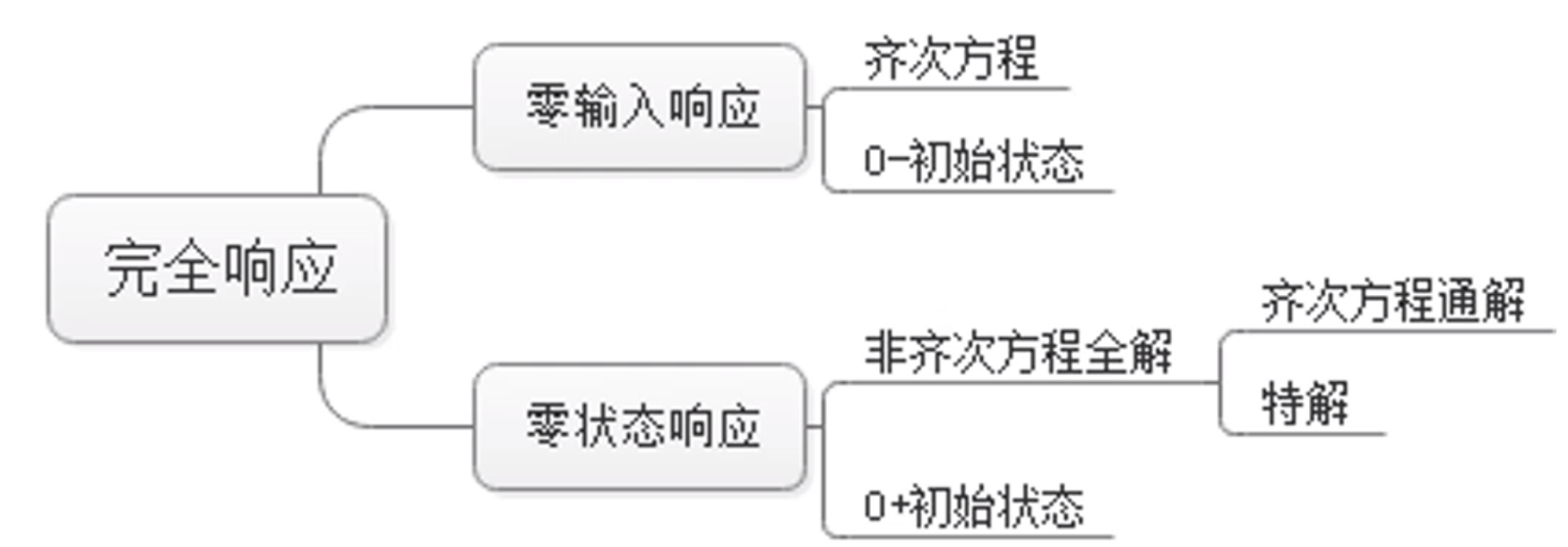
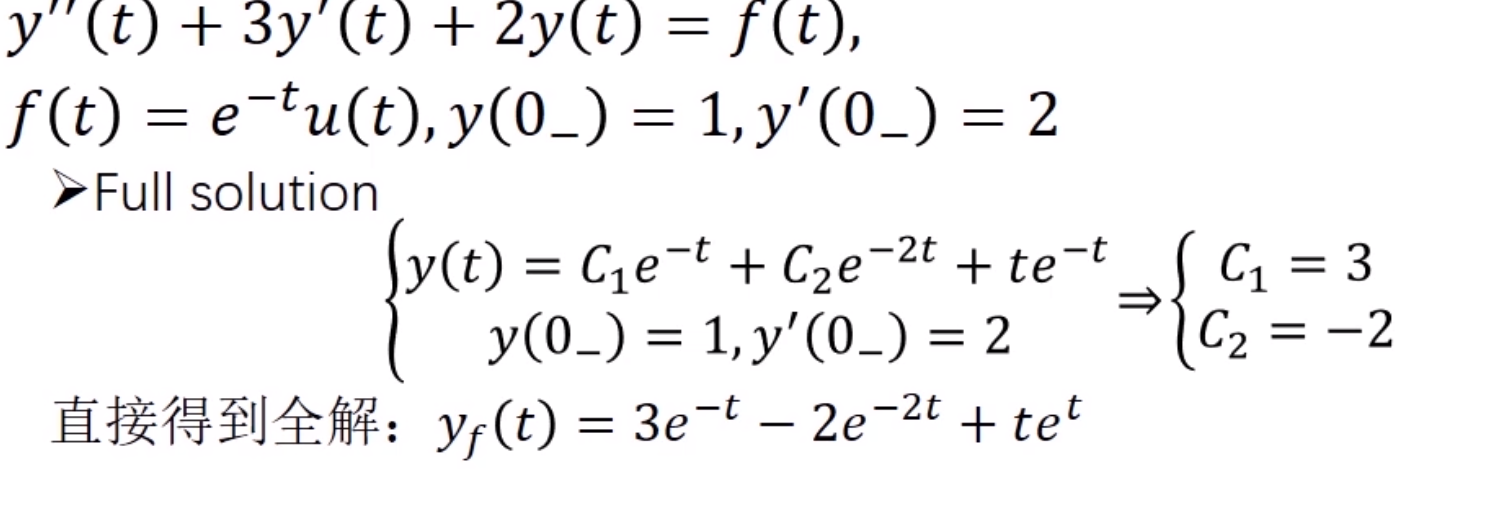





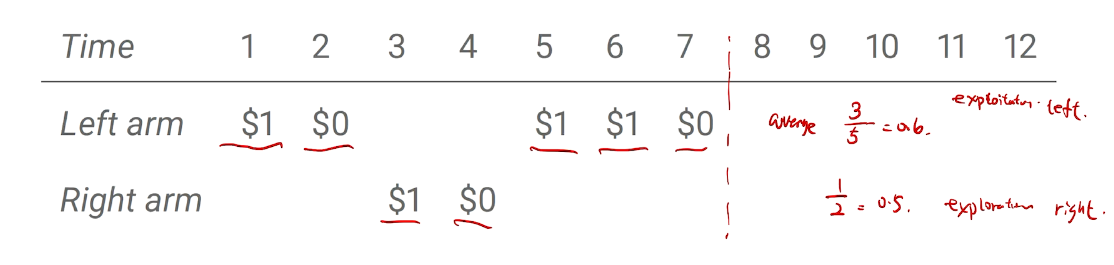











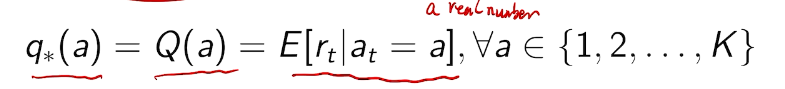
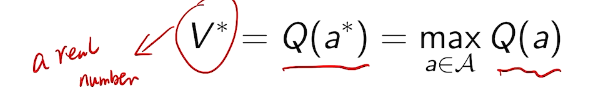
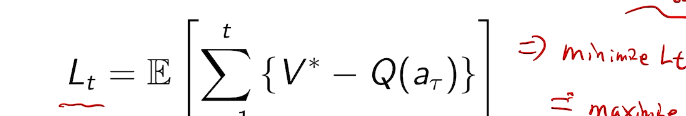
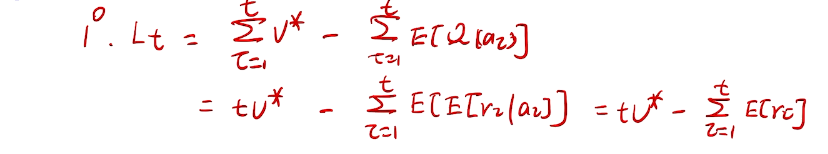

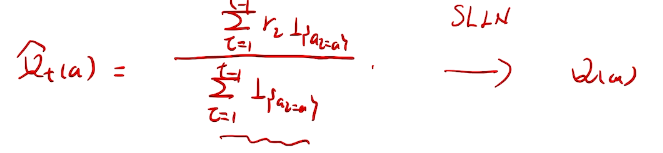


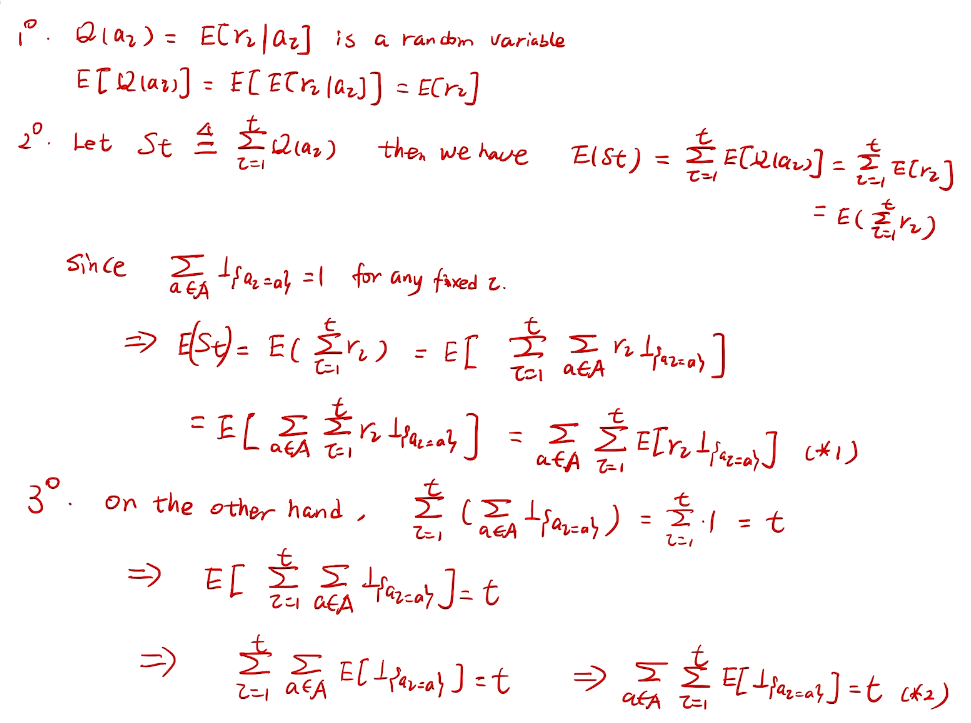
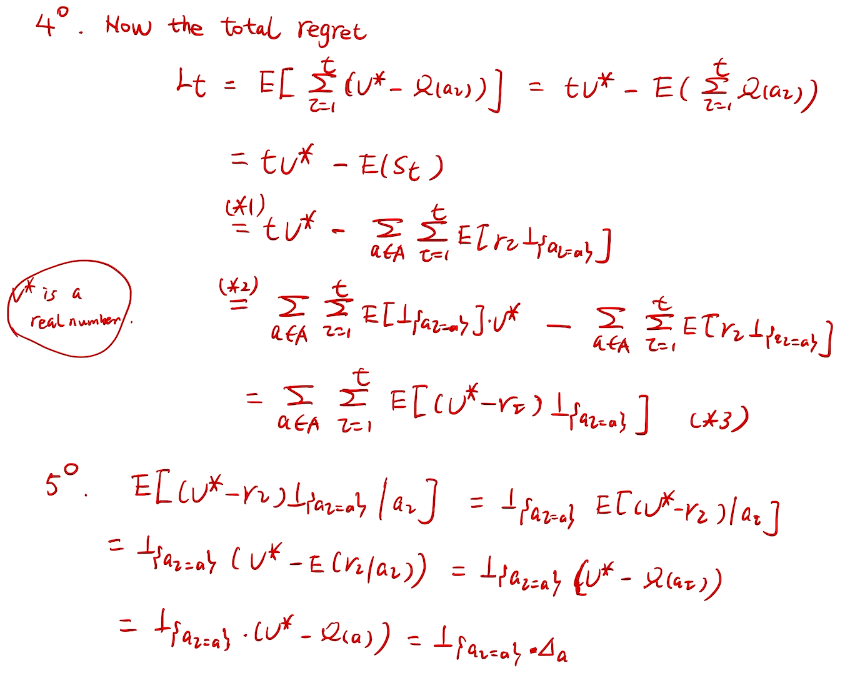
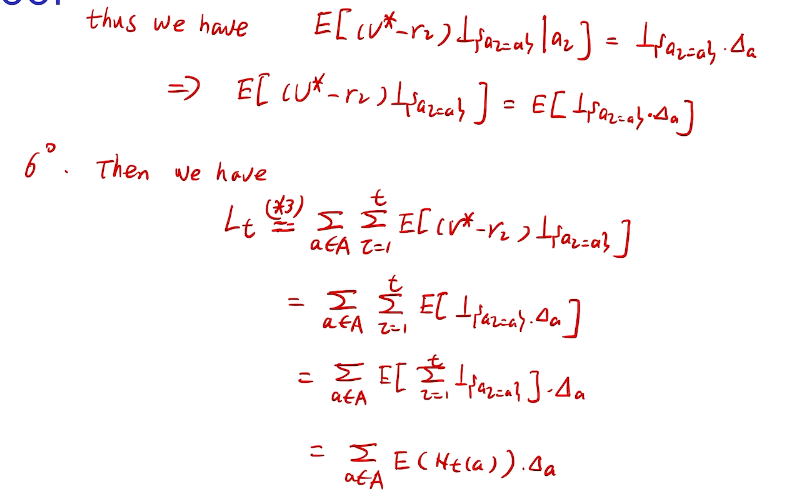
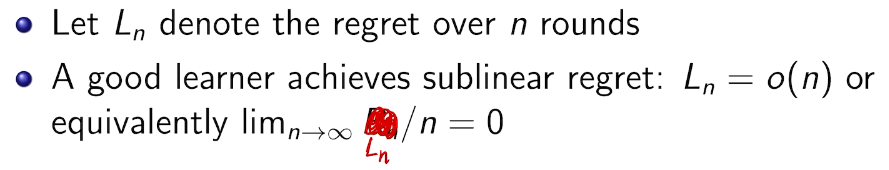



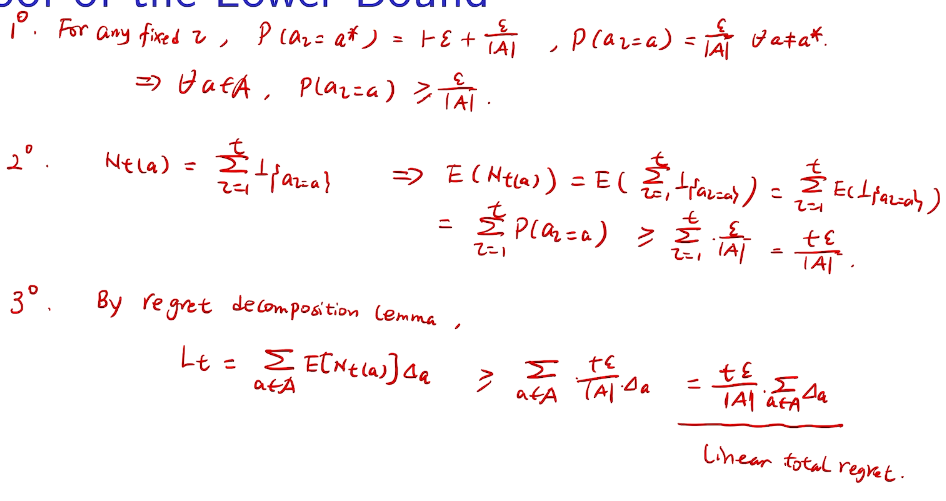

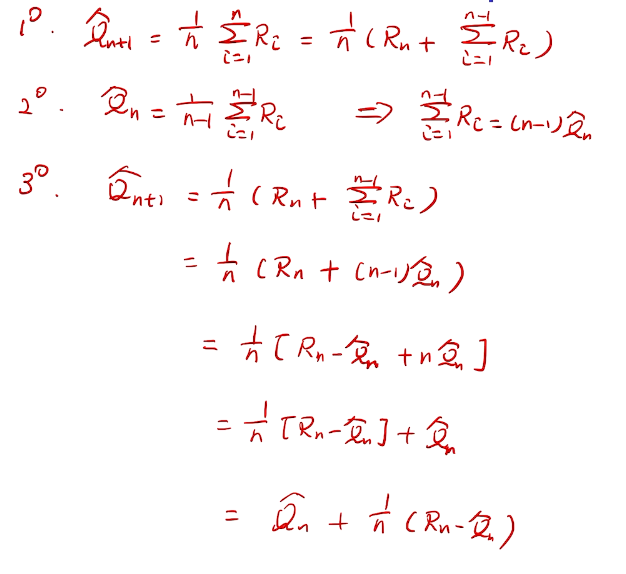



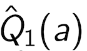 which is 0 in this case. but we can do 5.
which is 0 in this case. but we can do 5.


 ## bandit algorithm lower bounds(depends on gaps)
## bandit algorithm lower bounds(depends on gaps)







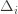 is small we will require more tries to know that action
is small we will require more tries to know that action 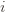 is suboptimal, and hence we will incur more regret. The second term represents a small constant number (the $1 + \pi^2 / 3$ part) that caps the number of times we’ll play suboptimal machines in excess of the first term due to unlikely events occurring. So the first term is like our expected losses, and the second is our risk.
is suboptimal, and hence we will incur more regret. The second term represents a small constant number (the $1 + \pi^2 / 3$ part) that caps the number of times we’ll play suboptimal machines in excess of the first term due to unlikely events occurring. So the first term is like our expected losses, and the second is our risk.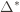 ), and let’s look at the worst case bound by maximizing it. In particular, we’re just finding the problem with the parameters which screw our bound as badly as possible, The gradient of the regret function is given by
), and let’s look at the worst case bound by maximizing it. In particular, we’re just finding the problem with the parameters which screw our bound as badly as possible, The gradient of the regret function is given by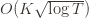
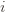 ,
, 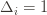 ), then we get a local maximum of
), then we get a local maximum of 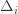 go to zero. But at the same time, if all the
go to zero. But at the same time, if all the 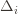 are small, then we shouldn’t be incurring much regret because we’ll be picking actions that are close to optimal!
are small, then we shouldn’t be incurring much regret because we’ll be picking actions that are close to optimal!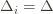 are the same, then another trivial regret bound is
are the same, then another trivial regret bound is 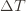 (why?). The true regret is hence the minimum of this regret bound and the UCB1 regret bound: as the UCB1 bound degrades we will eventually switch to the simpler bound. That will be a non-differentiable switch (and hence a critical point) and it occurs at
(why?). The true regret is hence the minimum of this regret bound and the UCB1 regret bound: as the UCB1 bound degrades we will eventually switch to the simpler bound. That will be a non-differentiable switch (and hence a critical point) and it occurs at 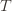 . Using the
. Using the 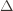 notation, the regret is then just
notation, the regret is then just 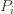 ‘s will bound the regret.
‘s will bound the regret.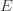 times. Recall further that the random variable
times. Recall further that the random variable 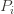 has as its value the index of the machine chosen. We denote by
has as its value the index of the machine chosen. We denote by 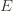 . And remember that we use an asterisk to denote a quantity associated with the optimal action (e.g.,
. And remember that we use an asterisk to denote a quantity associated with the optimal action (e.g., 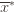 is the empirical mean of the optimal action).
is the empirical mean of the optimal action).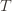 , the only way we know how to write down
, the only way we know how to write down 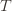 . Now we’re just going to pull some number
. Now we’re just going to pull some number 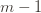 of plays out of that summation, keep it variable, and try to optimize over it. Since we might play the action fewer than
of plays out of that summation, keep it variable, and try to optimize over it. Since we might play the action fewer than 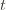 times overall, this requires an inequality.
times overall, this requires an inequality.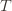 in round
in round 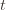 and we’ve already played
and we’ve already played 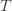 at least
at least 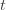 times. Now we’re going to focus on the inside of the summation, and come up with an event that happens at least as frequently as this one to get an upper bound. Specifically, saying that we’ve picked action
times. Now we’re going to focus on the inside of the summation, and come up with an event that happens at least as frequently as this one to get an upper bound. Specifically, saying that we’ve picked action 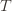 in round
in round 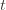 means that the upper bound for action
means that the upper bound for action 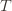 exceeds the upper bound for every other action. In particular, this means its upper bound exceeds the upper bound of the best action (and
exceeds the upper bound for every other action. In particular, this means its upper bound exceeds the upper bound of the best action (and 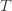 might coincide with the best action, but that’s fine). In notation this event is
might coincide with the best action, but that’s fine). In notation this event is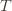 in round
in round 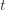 by
by 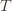 (though not necessarily vice versa), we have
(though not necessarily vice versa), we have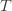 exceeds that of the optimal machine, it is also the case that the maximum upper bound for action
exceeds that of the optimal machine, it is also the case that the maximum upper bound for action 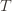 we’ve seen after the first
we’ve seen after the first 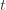 trials exceeds the minimum upper bound we’ve seen on the optimal machine (ever). But on round
trials exceeds the minimum upper bound we’ve seen on the optimal machine (ever). But on round 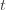 we don’t know how many times we’ve played the optimal machine, nor do we even know how many times we’ve played machine
we don’t know how many times we’ve played the optimal machine, nor do we even know how many times we’ve played machine 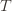 (except that it’s more than
(except that it’s more than 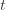 ). So we try all possibilities and look at minima and maxima. This is a pretty crude approximation, but it will allow us to write things in a nicer form.
). So we try all possibilities and look at minima and maxima. This is a pretty crude approximation, but it will allow us to write things in a nicer form.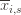 the random variable for the empirical mean after playing action
the random variable for the empirical mean after playing action 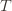 a total of
a total of  times, and
times, and 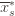 the corresponding quantity for the optimal machine. Realizing everything in notation, the above argument proves that
the corresponding quantity for the optimal machine. Realizing everything in notation, the above argument proves that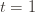 to
to 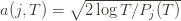 . This will become clear later, but it means we can replace
. This will become clear later, but it means we can replace 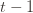 with
with 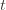 and thus have
and thus have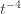 . Likewise, (2) is the event that the empirical mean payoff of action
. Likewise, (2) is the event that the empirical mean payoff of action 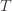 is larger than the upper confidence bound, which also occurs with probability
is larger than the upper confidence bound, which also occurs with probability 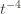 . We will see momentarily that (3) is impossible for a well-chosen
. We will see momentarily that (3) is impossible for a well-chosen 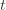 (which is why we left it variable), but in any case the claim is that one of these three events must occur. For if they are all false, we have
(which is why we left it variable), but in any case the claim is that one of these three events must occur. For if they are all false, we have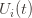 plus whatever the probability of (3) being true is. But as we said, we’ll pick
plus whatever the probability of (3) being true is. But as we said, we’ll pick 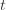 to make (3) always false. Indeed
to make (3) always false. Indeed 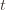 depends on which action
depends on which action 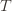 is being played, and if
is being played, and if 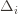 we have
we have