2 great law
Amdahi
Amdahi law defines the speedup formula after the parallelization of the serial system.
The defination of the speedup: \(Speedup = \frac{Time\ before\ optimized} {Time\ after\ optimized}\). The higher the speedup, the better the optimization.
Proof: The time after optimization: \(T_n=T_1(F+\frac1{n(1-F)})\), where \(T_1\) stands for the time before optimization, F is the percentage of serialized program,\((1-F)\) is the percentage of paralized program,n is the number of processor number. Take those into the equation we have \(\frac{T_1}{T_n}\),namely \(\frac{1}{(F + \frac{1}{n(1-F)})}\).
From the equation we can induce that the \(Speedup\) is inversely related with the \(F\). Also, from the equation, we can see that adding processor's number is just another method of providing \(Speedup\). Besides, lowering \(F\) can have the same effect.
For example in the \(ASC19\), besides merely applying the \(MPI\) parameter modification. The serialized part like initialization and special operation on the Qubits.
Gustafson
Gustafson is another important ways of evaluating the speedup rate
define the serialized processing time \(a\),parallelized processing time \(b\), namely single CPU situation, so the executing time \(a+b\) overall executing time \(a+nb,\) n denotes CPU number.
define the propertion F of a out of the executing time \(F=\frac{a}{(a+b)}\)
we get the final speedup rate. \(s(n)=a+\frac{nb}{a}+b=\frac a{a+b} + \frac{nb}{a+b} = F + \frac{n(b-a+a)}{a+b }= F + n(1-F)\)
From the equation, we have if the serialized part is tiny enough, $s(n) equals to the number of the CPU, so reducing the serialized part make sense, as well as adding the CPU core.
difference between two criteria
Two different law treats the parallel program from 2 different angles. Amdahi said that when the serial ratio is fixed, there is an upper limit by adding a CPU. By reducing the serial ratio and increasing the number of CPUs, the acceleration ratio can be improved. Gustafson is saying that when serial comparison tends to be very small, it can be seen from the formula that adding cpu can improve the speedup ratio
Multi-threaded features
Because of the inconsistency and security of data in a multi-threaded environment, some rule-based control is required. Java's memory model JMM regulates the effective and correct execution of multi-threading, and JMM is precisely the atomicity, visibility, and Orderly, so this blog introduces some multi-threaded atomicity, visibility and order.
Atomic
For single-threaded, it is indeed atomic, such as an int variable, change the value, it is the value when reading, this is very normal, we go to the system to run, it is also the same, because our operation Most of the system is 32-bit and 64-bit, int type 4 bytes, that is, 32-bit, but you can try the value of long type, long type is 8 bytes, which is 64-bit, if both threads Read and write it? In a multi-threaded environment, a thread changes the value of the long type and then reads it. The obtained value is not necessarily the value just changed, because your system may be 32-bit, and the long type is 64-bit. Yes, if both threads read and write to the long type, this will happen.
Visibility
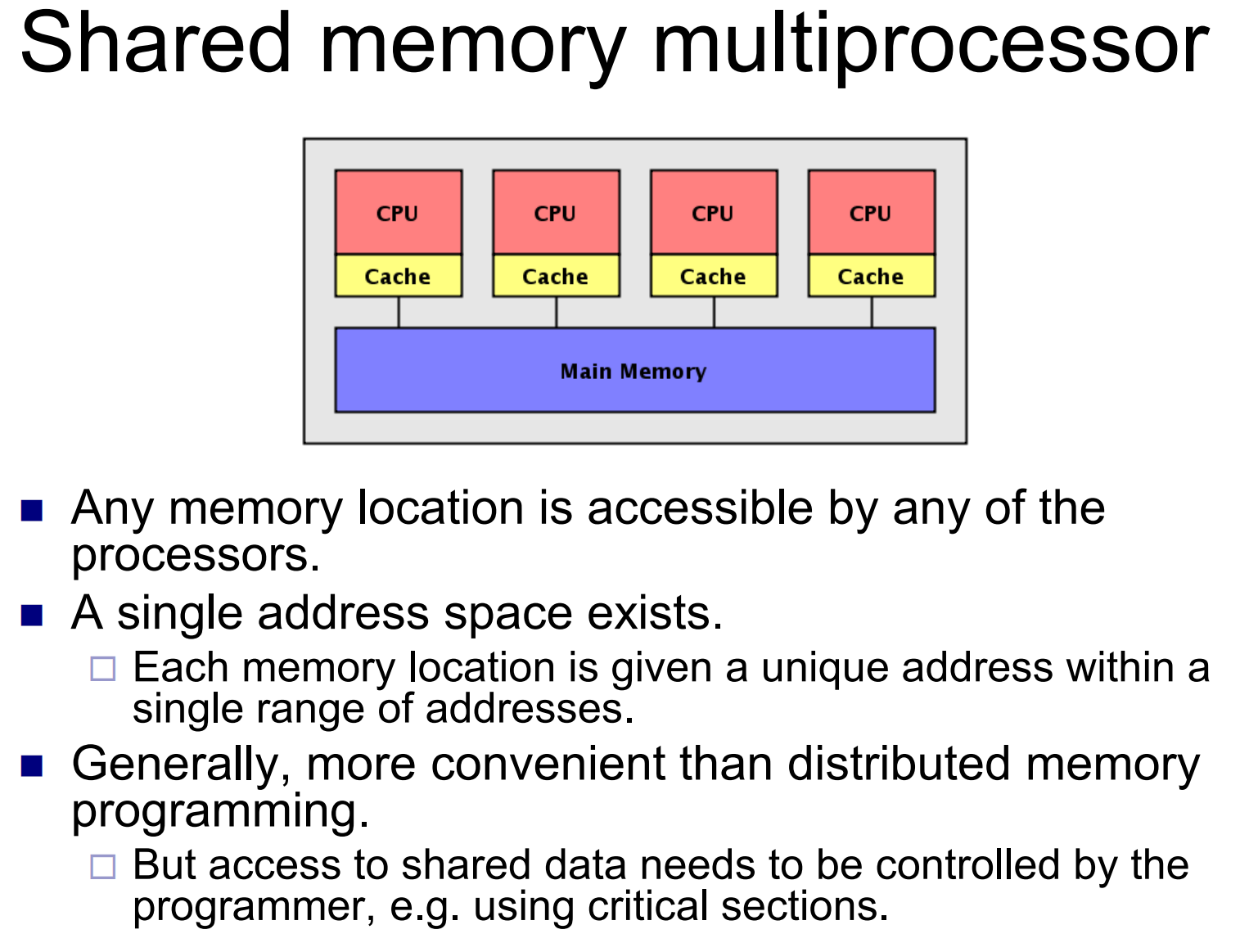
How to understand visibility? First of all, there is no visibility for single-threaded. Visibility is for multi-threaded. For example, if one thread has changed, does another thread know that the thread has changed, this is visibility . For example, the variable a is a shared variable. The variable a on cpu1 is cache optimized, and the variable a is placed in the cache. At this time, the thread on the other cpu2 changes the variable a. This operation is for cpu1. The thread is not visible, because cpu1 has been cached, so the thread on cpu1 reads the variable a from the cache, and found that the value read on cpu2 is not consistent.
Ordered
For single-threaded, the code execution of a thread is in order, which is true, but in a multi-threaded environment may not be necessary. Because in a multi-threaded environment instruction rearrangement may occur. In other words, in a multi-threaded environment, code execution is not necessarily ordered.
Since disorder is caused by rearrangement, then all instructions will be rearranged? of course not. The rearrangement follows: Happen-Before rule.

























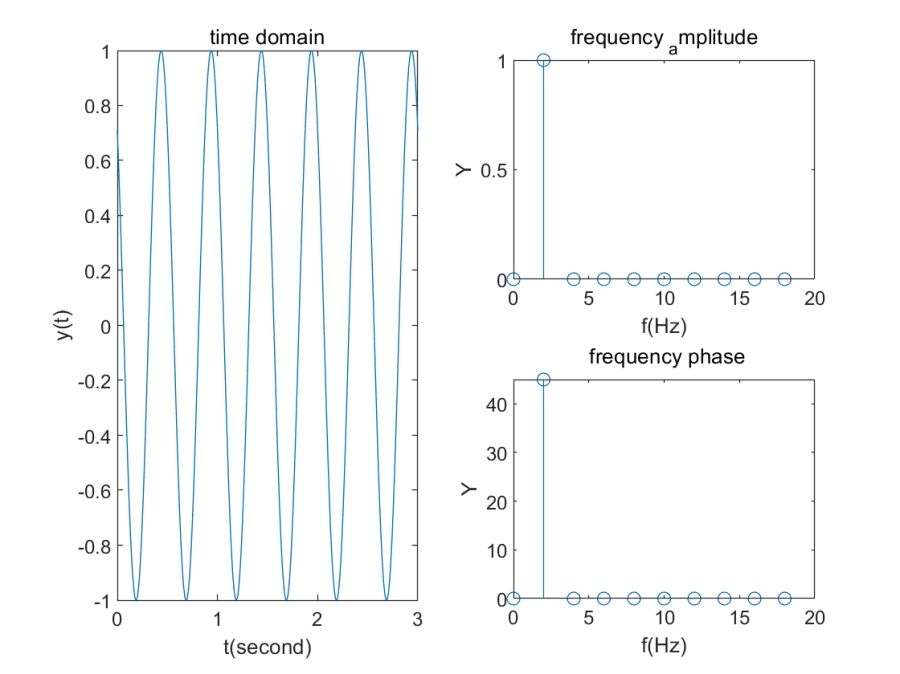
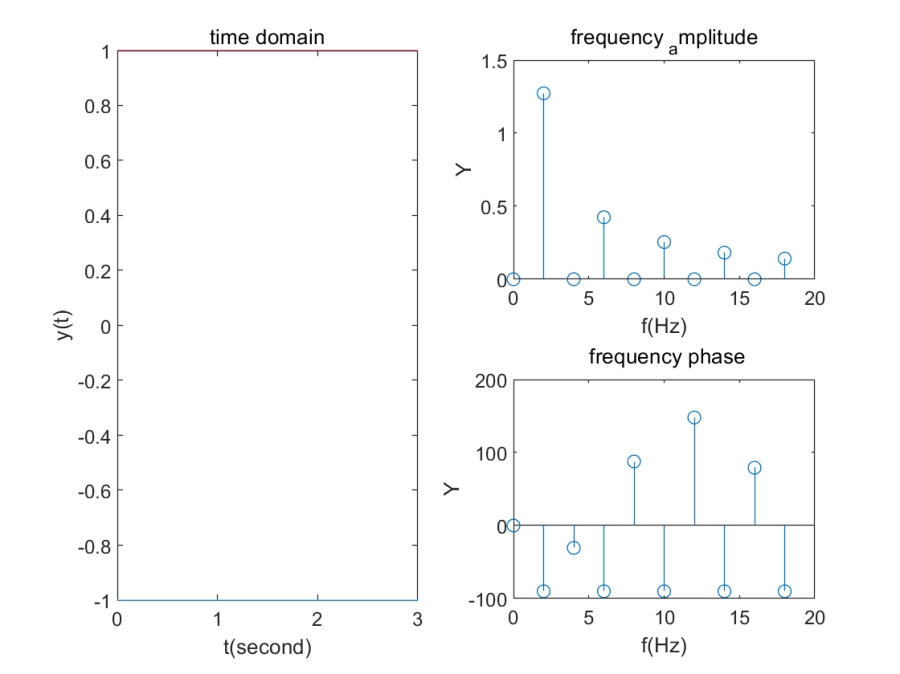
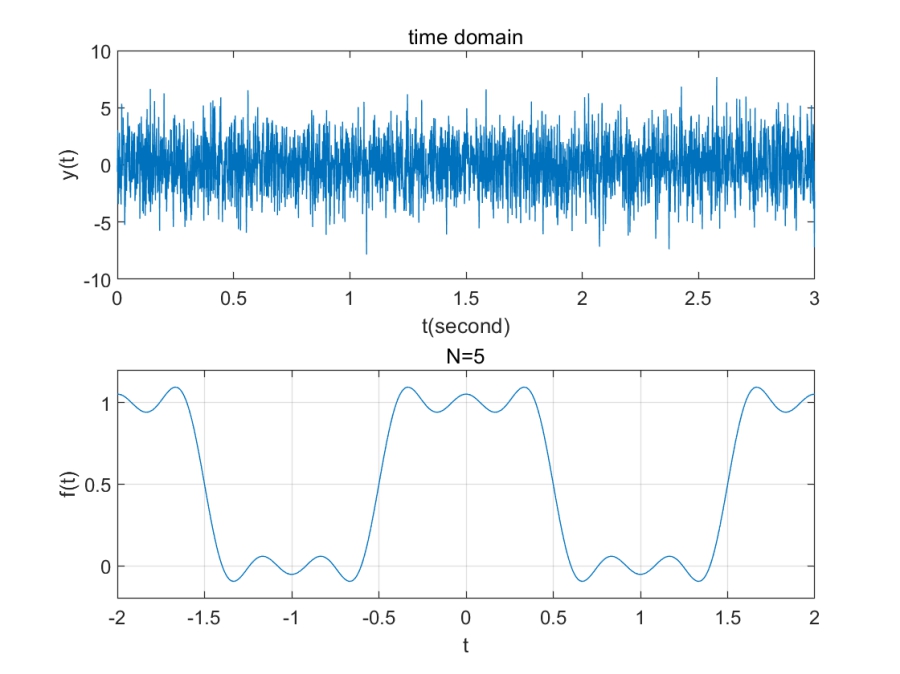
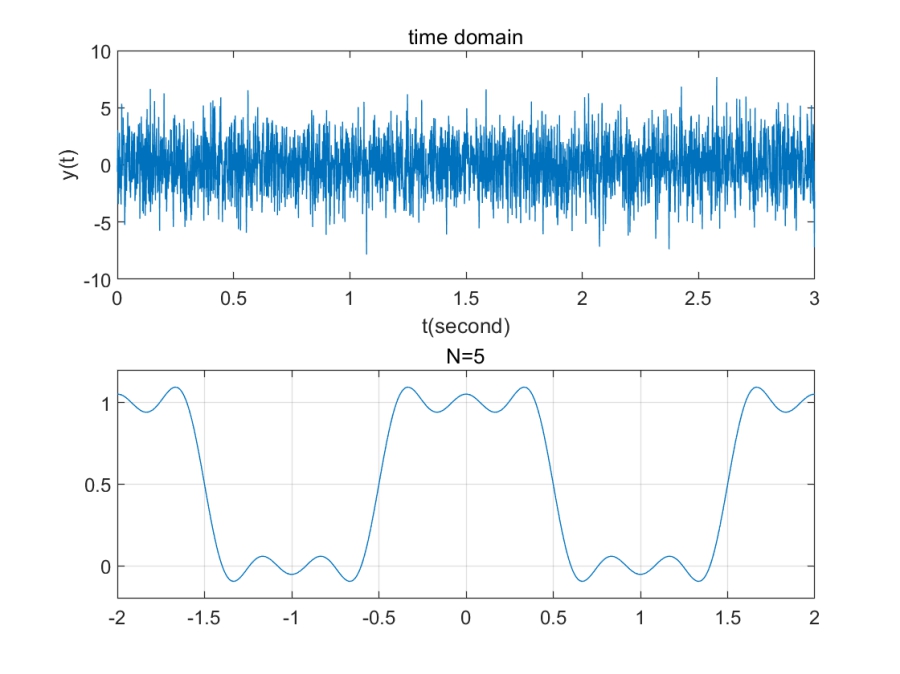
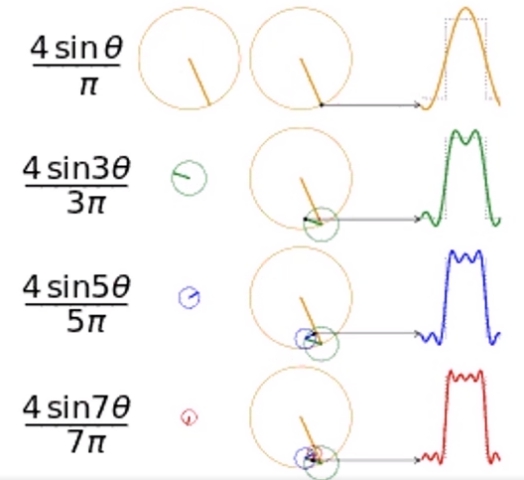 一种看时域图的角度
一种看时域图的角度