Category: Study 📕

Posted on

Growing A Test Corpus with Bonsai Fuzzing @ICSE'21

For generating synthesization automatically based on the ChocoPy dialect which I'm in great need of, the author of ChocoPy published their tricky counterpart to C-smith/ Fuzzy Grammer Generator called Bonsal Fuzzing.

Problems and Pair Review

Instead of Fuzz-then-reduce method, the corpus bottom up generation is already concise. enough and can touch much of the corner test cases.

  1. Bounded Exhaustive Testing: input of bounded size are generated systematically but not enumerated exhaustively
  2. So enumerate the k-path with the grammar.
  3. JPF-SE explores the space of program paths, for bounding the size of a comprehensive test suite that covers a diverse set of program paths
  4. different kind of strategies of fuzzing: Coverage-Guided Fuzzing, Specialized Compiler Fuzing, Grammar-based, Semantic Fuzzing(Zest)
  5. Test-Case Reduction by Hieachical delta debugging

Implementation

  1. Bounded Grammar Fuzzers: Bound iteration by idens, items, depths number.

  2. Coverage-Guided Bounded Grammar Fuzzing


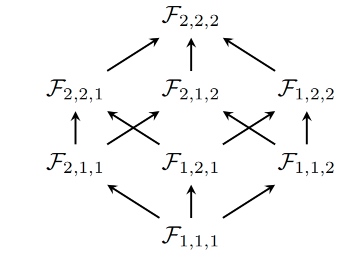
    The lattice of coverage-guided size-bounded grammar-based fuzzers $F_{m,n,d}$, ordered by three size bounds on the syntax of the test cases they produce: number of unique identifiers m, maximum sequence length n, and maximum nesting depth d.

Test cases flow along directed edges: the inputs generated by each fuzzer are used as the seed inputs to its successors. The result of bonsai fuzzing is the corpus produced by the top-most element.

  1. Bonsai fuzzing with extended lattice


Posted on

Encountering `::signbit` stuff not passing to `math.h` in MacOS 12.4

TL;DR

/Applications/Xcode.app/Contents/Developer/Toolchains/XcodeDefault.xctoolchain/usr/bin/../include/c++/v1/cmath:317:9: error: no member named 'signbit' in the global namespace
using ::signbit;
      ~~^
/Applications/Xcode.app/Contents/Developer/Toolchains/XcodeDefault.xctoolchain/usr/bin/../include/c++/v1/cmath:318:9: error: no member named 'fpclassify' in the global namespace
using ::fpclassify;
      ~~^
/Applications/Xcode.app/Contents/Developer/Toolchains/XcodeDefault.xctoolchain/usr/bin/../include/c++/v1/cmath:319:9: error: no member named 'isfinite' in the global namespace
using ::isfinite;
      ~~^
/Applications/Xcode.app/Contents/Developer/Toolchains/XcodeDefault.xctoolchain/usr/bin/../include/c++/v1/cmath:320:9: error: no member named 'isinf' in the global namespace
using ::isinf;
      ~~^
/Applications/Xcode.app/Contents/Developer/Toolchains/XcodeDefault.xctoolchain/usr/bin/../include/c++/v1/cmath:321:9: error: no member named 'isnan' in the global namespace
using ::isnan;
      ~~^
/Applications/Xcode.app/Contents/Developer/Toolchains/XcodeDefault.xctoolchain/usr/bin/../include/c++/v1/cmath:322:9: error: no member named 'isnormal' in the global namespace
using ::isnormal;
      ~~^
/Applications/Xcode.app/Contents/Developer/Toolchains/XcodeDefault.xctoolchain/usr/bin/../include/c++/v1/cmath:323:9: error: no member named 'isgreater' in the global namespace
using ::isgreater;
      ~~^
/Applications/Xcode.app/Contents/Developer/Toolchains/XcodeDefault.xctoolchain/usr/bin/../include/c++/v1/cmath:324:9: error: no member named 'isgreaterequal' in the global namespace
using ::isgreaterequal;
      ~~^
/Applications/Xcode.app/Contents/Developer/Toolchains/XcodeDefault.xctoolchain/usr/bin/../include/c++/v1/cmath:325:9: error: no member named 'isless' in the global namespace
using ::isless;
      ~~^
/Applications/Xcode.app/Contents/Developer/Toolchains/XcodeDefault.xctoolchain/usr/bin/../include/c++/v1/cmath:326:9: error: no member named 'islessequal' in the global namespace
using ::islessequal;
      ~~^
/Applications/Xcode.app/Contents/Developer/Toolchains/XcodeDefault.xctoolchain/usr/bin/../include/c++/v1/cmath:327:9: error: no member named 'islessgreater' in the global namespace
using ::islessgreater;
      ~~^
/Applications/Xcode.app/Contents/Developer/Toolchains/XcodeDefault.xctoolchain/usr/bin/../include/c++/v1/cmath:328:9: error: no member named 'isunordered' in the global namespace
using ::isunordered;
      ~~^
/Applications/Xcode.app/Contents/Developer/Toolchains/XcodeDefault.xctoolchain/usr/bin/../include/c++/v1/cmath:329:9: error: no member named 'isunordered' in the global namespace
using ::isunordered;
      ~~^

When I was compiling LLVM recently I found this, it may be because my CommandLineTool is outdated as described in stackoverflow. And I reinstalled it with following code added.

using ::signbit _LIBCPP_USING_IF_EXISTS;
using ::fpclassify _LIBCPP_USING_IF_EXISTS;
using ::isfinite _LIBCPP_USING_IF_EXISTS;
using ::isinf _LIBCPP_USING_IF_EXISTS;
using ::isnan _LIBCPP_USING_IF_EXISTS;
using ::isnormal _LIBCPP_USING_IF_EXISTS;
using ::isgreater _LIBCPP_USING_IF_EXISTS;
using ::isgreaterequal _LIBCPP_USING_IF_EXISTS;
using ::isless _LIBCPP_USING_IF_EXISTS;
using ::islessequal _LIBCPP_USING_IF_EXISTS;
using ::islessgreater _LIBCPP_USING_IF_EXISTS;
using ::isunordered _LIBCPP_USING_IF_EXISTS;
using ::isunordered _LIBCPP_USING_IF_EXISTS;

_LIBCPP_USING_IF_EXISTS is defined as # define _LIBCPP_USING_IF_EXISTS __attribute__((using_if_exists)), simply pass if no defined in the global namespace.

Then the following code output error

using _Lim = numeric_limits<_IntT>;

add another header in 

#include <limits>

Then comes to the std::isnan using bypassing no definition error in llvm/lib/Support/NativeFormatting.cpp.

error: expected unqualified-id for std::isnan(N)

just drop the std::

The full formula for riscv-rvv-llvm is located in https://github.com/victoryang00/homebrew-riscv, if anything above happens, do as the above specifies.

Posted on

UCLID5: Integrating Modeling, Verification, Synthesis, and Learning

When I was browsing keystones‘ paper, they are applying a verification model called UCLID5, a new software toolkit based on z3 written in scala for the formal modeling, specification, verification, and synthesis of computational systems. The augmented efforts are merely making architectural implementations like NAPOT/S mode world change/exceptions in pmp reg mapping policy to Hoare logic and do the verification. To a greater extent, the Y86-64 introduced in CSAPP is verified by UCLID5, too.

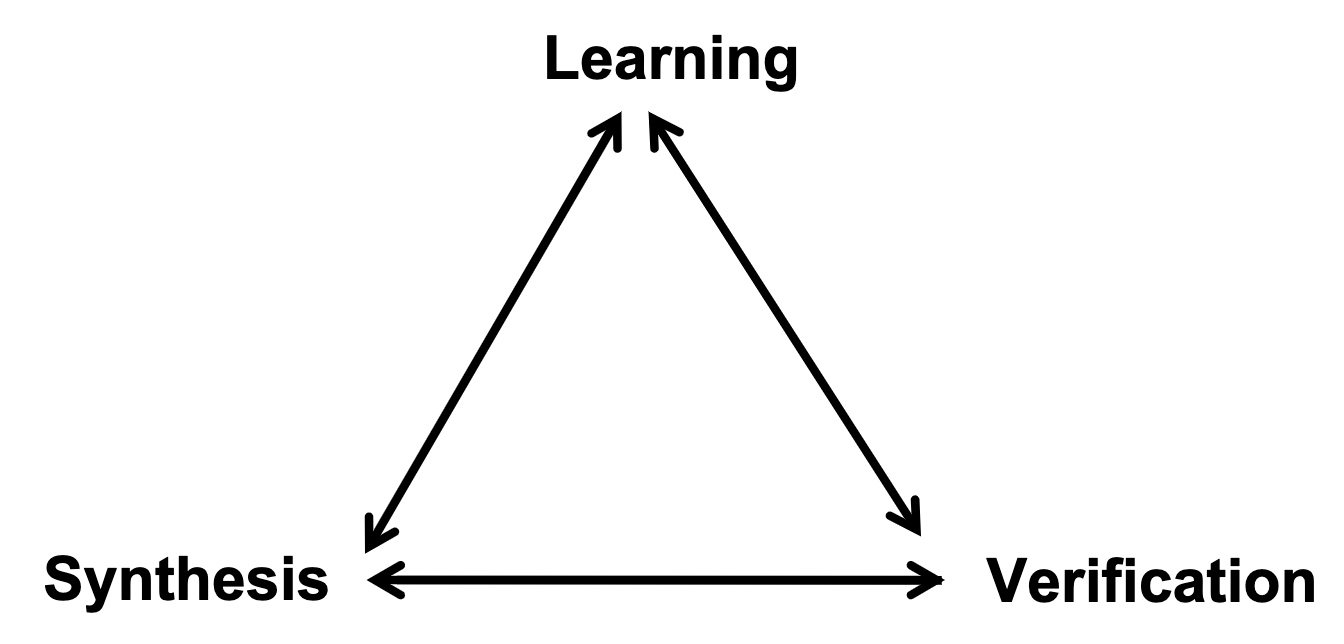
The Goals

  1. Enabling modular modeling of finite and infinite-state transition systems across a range of concurrency models and background logical theories.
  2. Performing a highly-automated, compositional verification of a diverse class of specifications, including pre/post conditions, assertions, invariant, LTL, refinement and hyperproperties
  3. Integrating modeling and verification with algorithmic synthesis and learning.

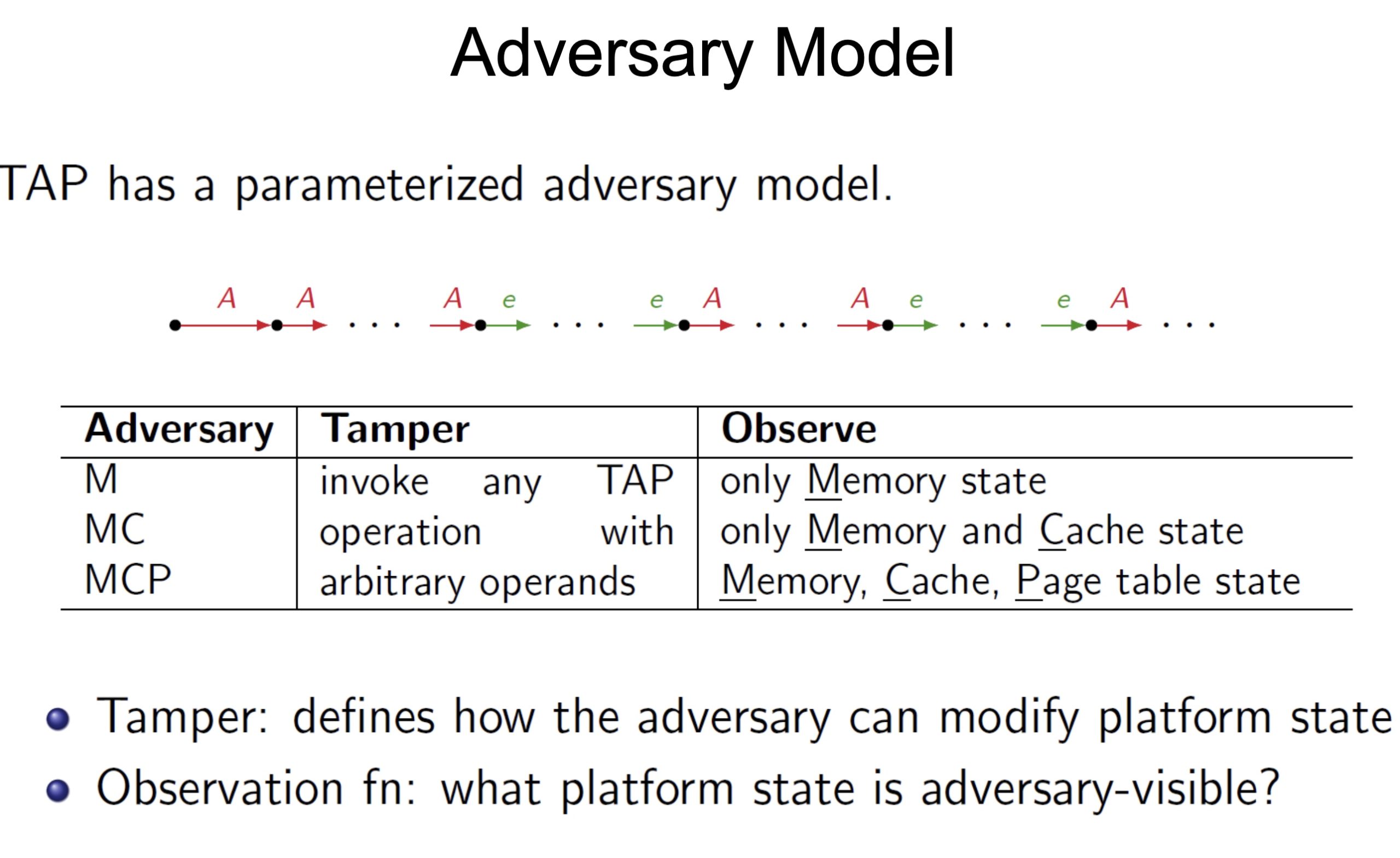
threat models

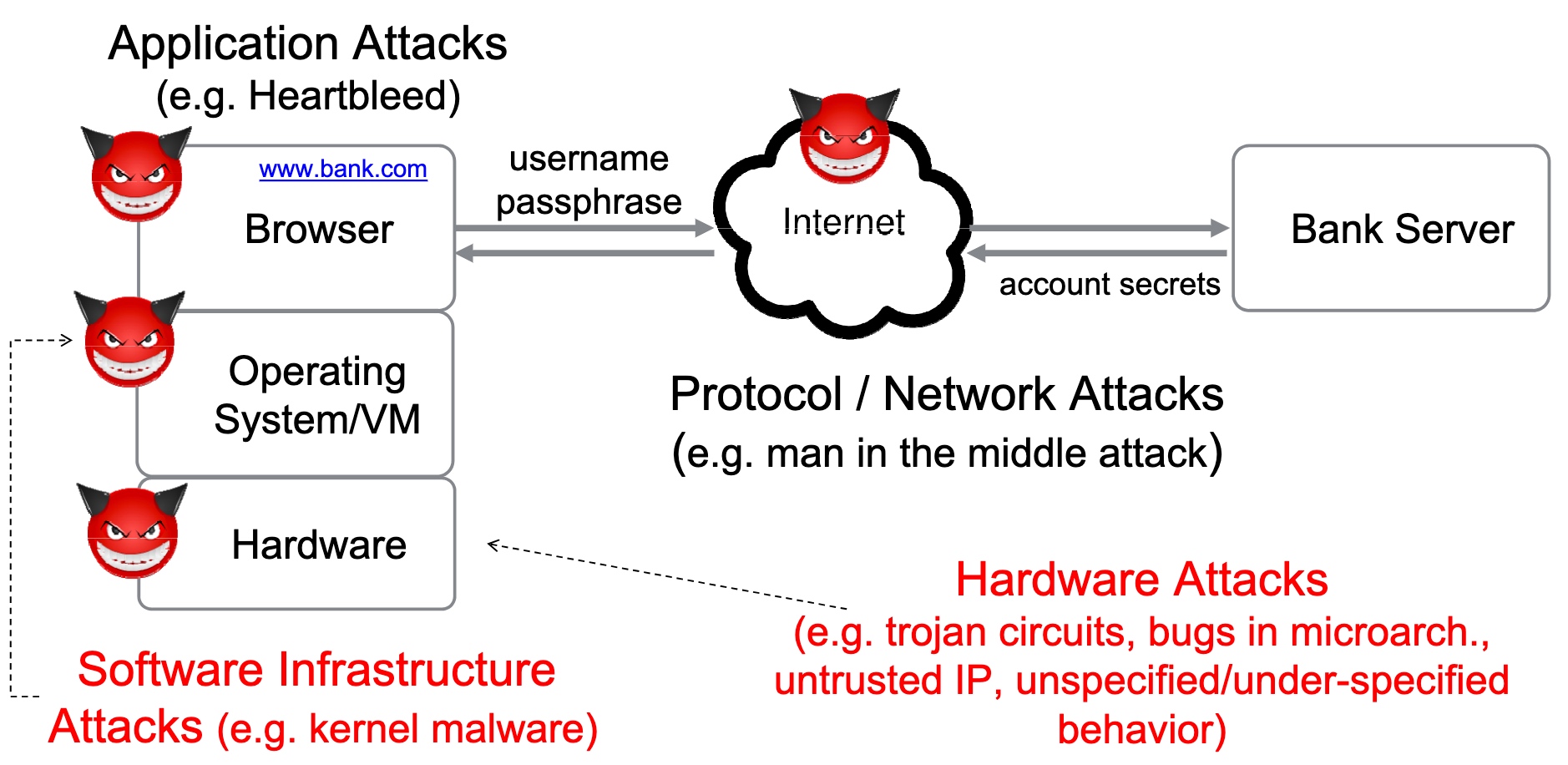
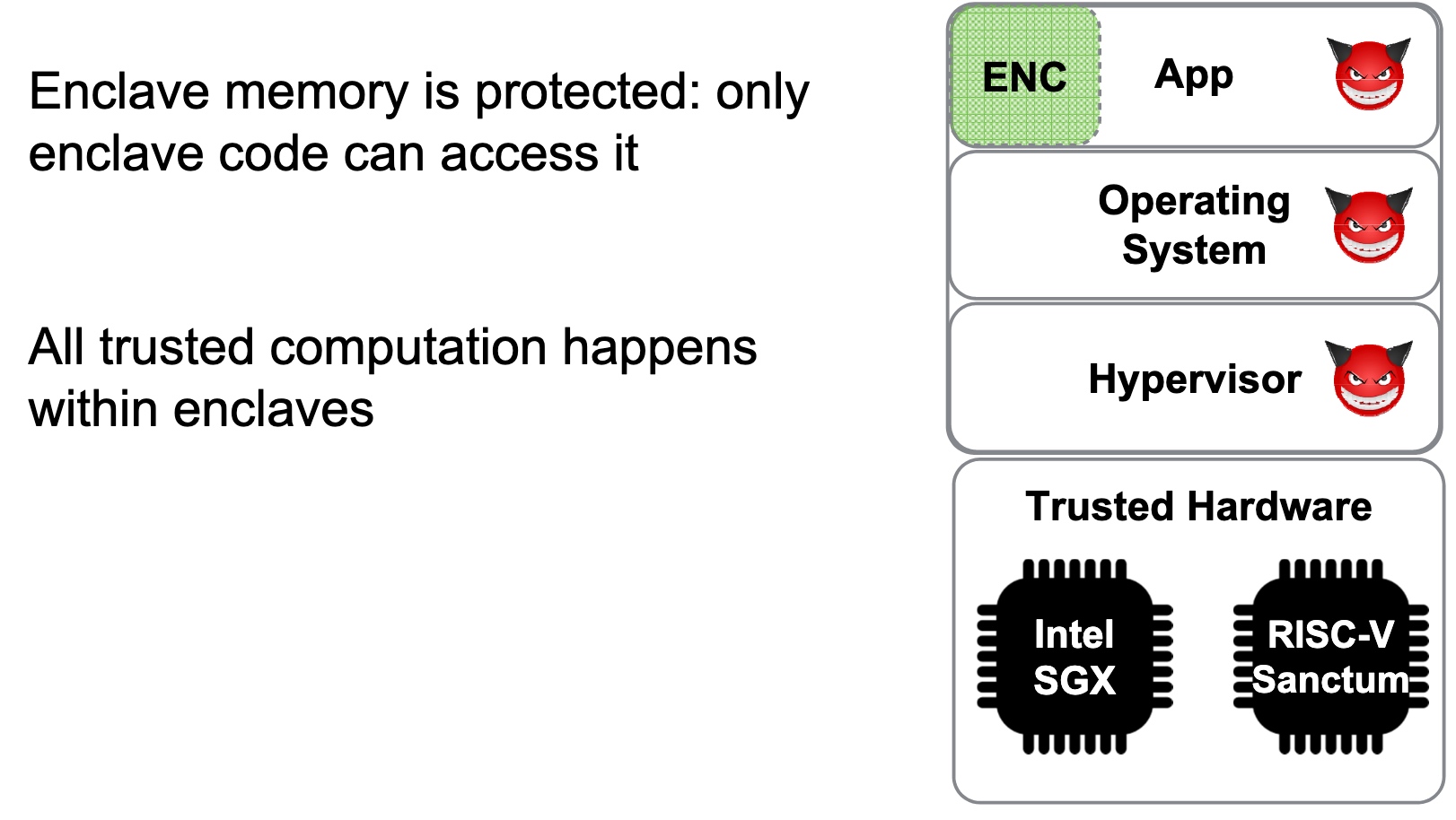
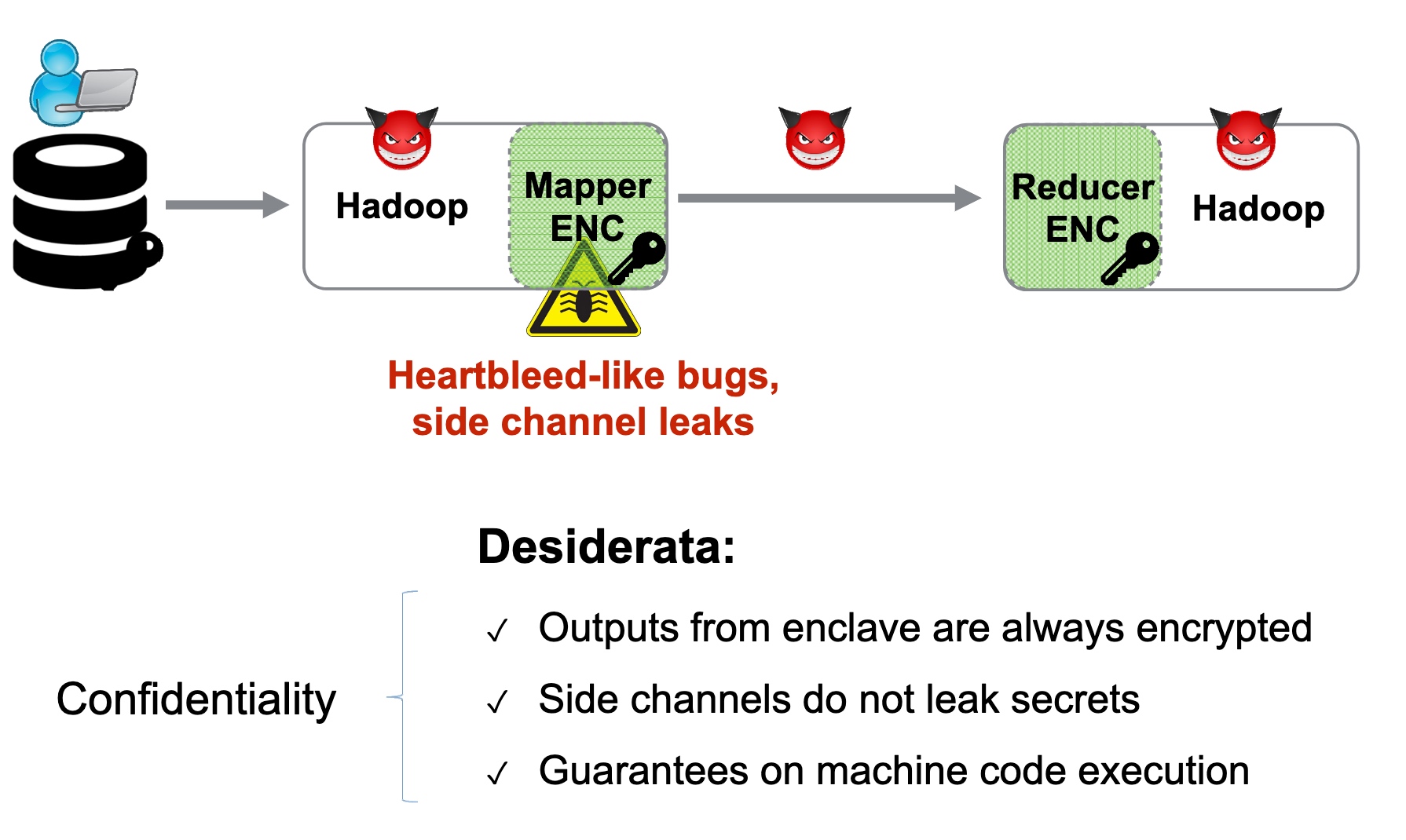
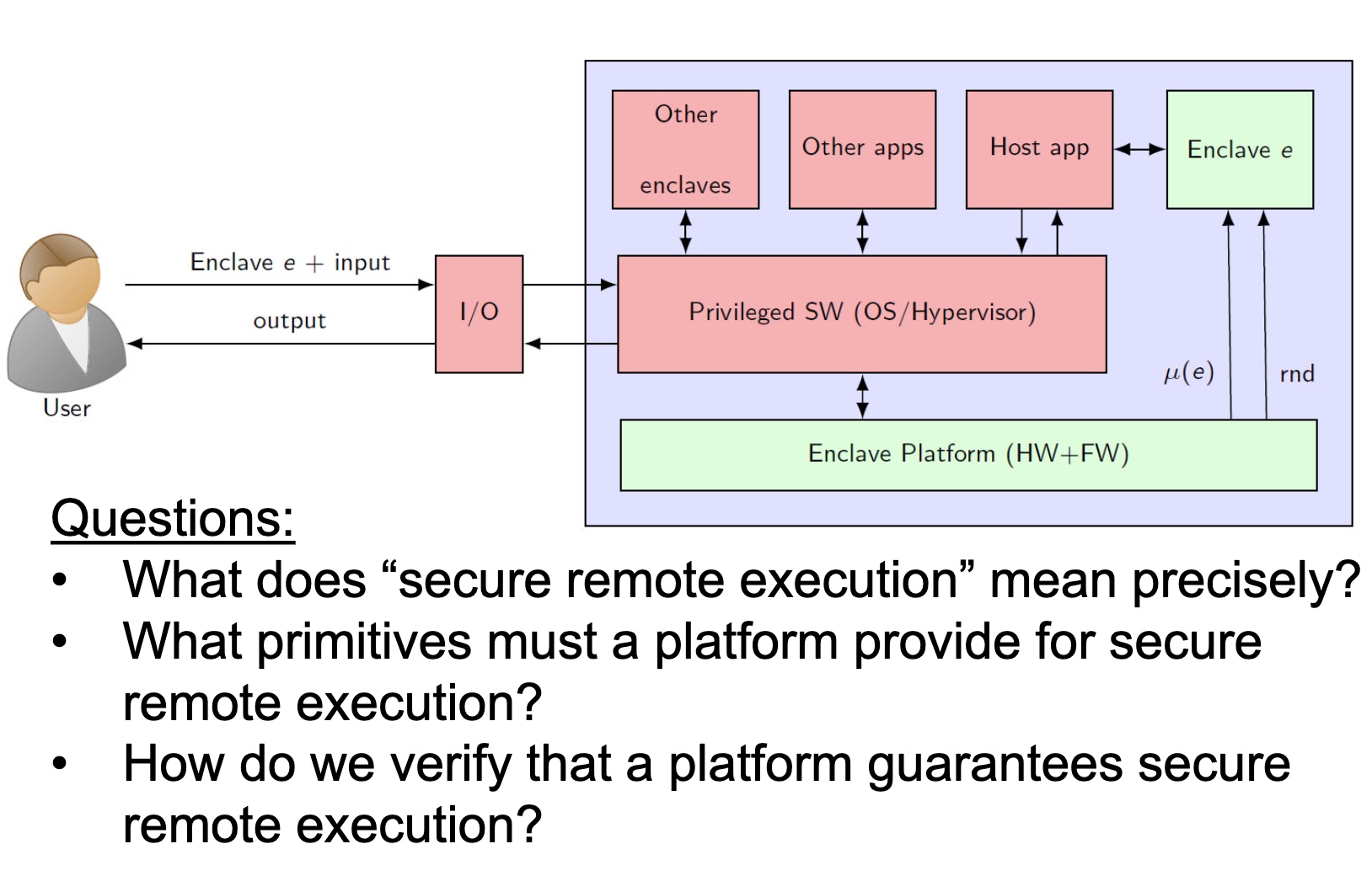
SRE

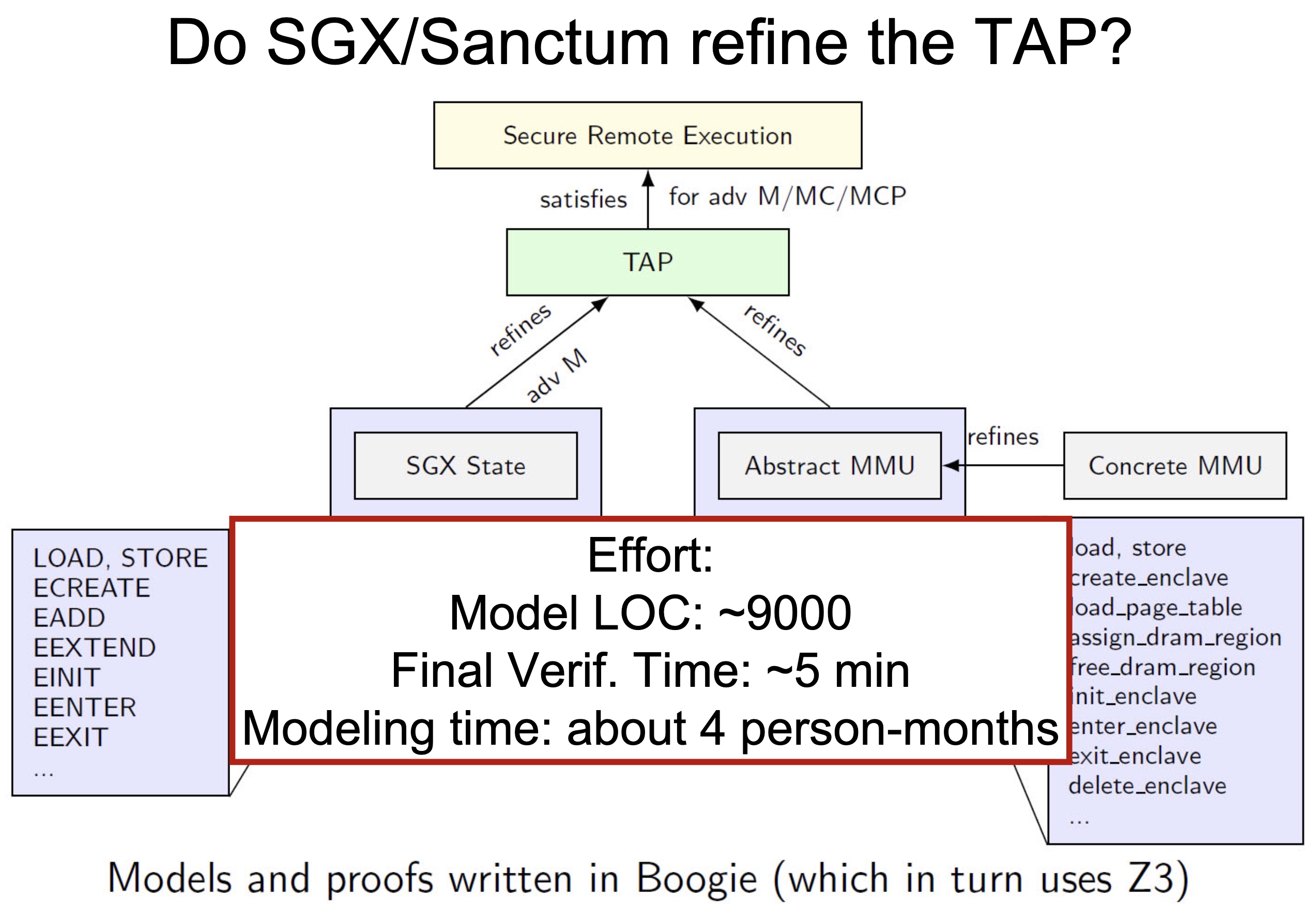
Heartbleed-like attack, side channels, and Meltdown/Spectre are also cast a lot on SGX/TEE. Stuff like secure remote extensions using trusted platforms is introduced. They formalized the enclave platform and made remote execution trustworthy.

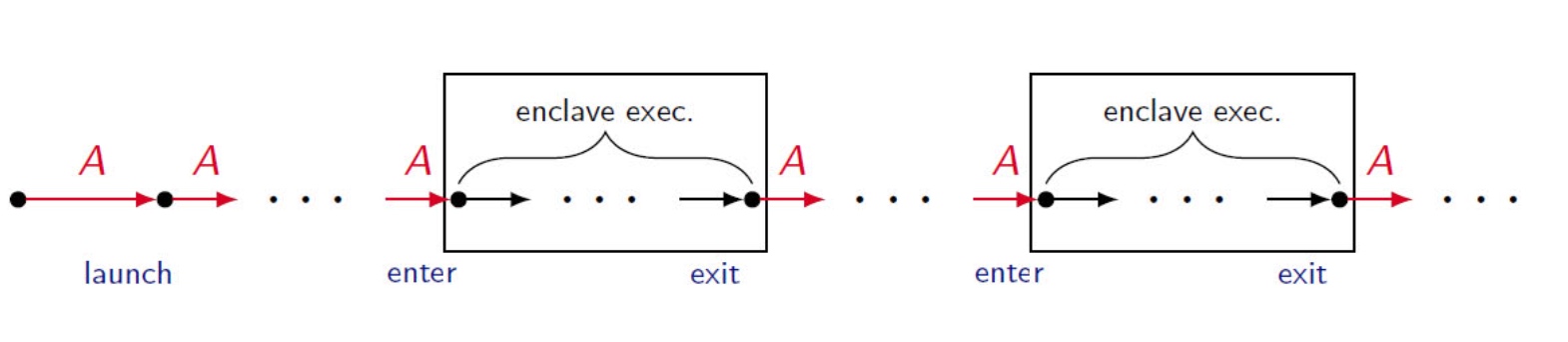
embodying enclave and adversary






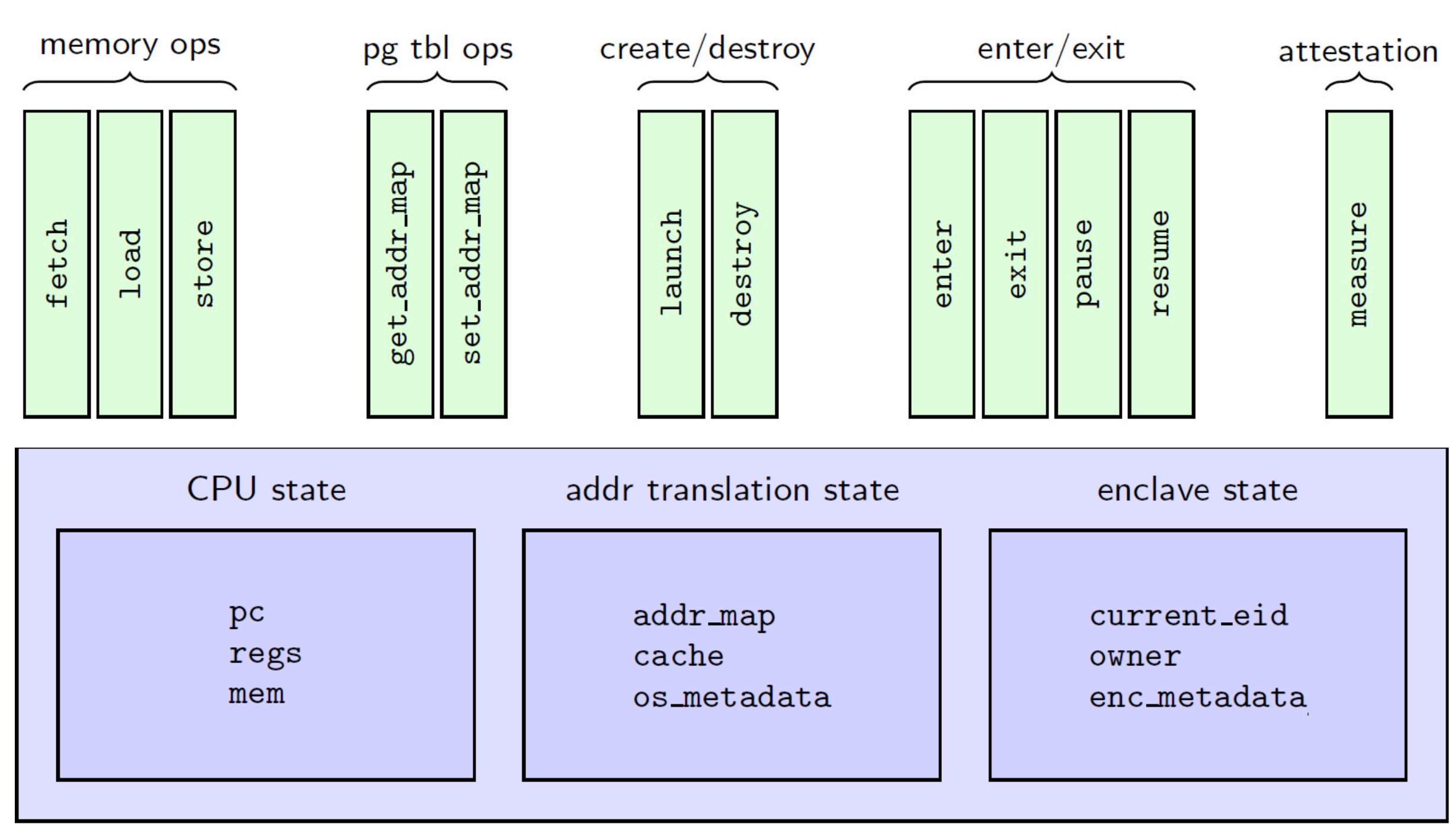
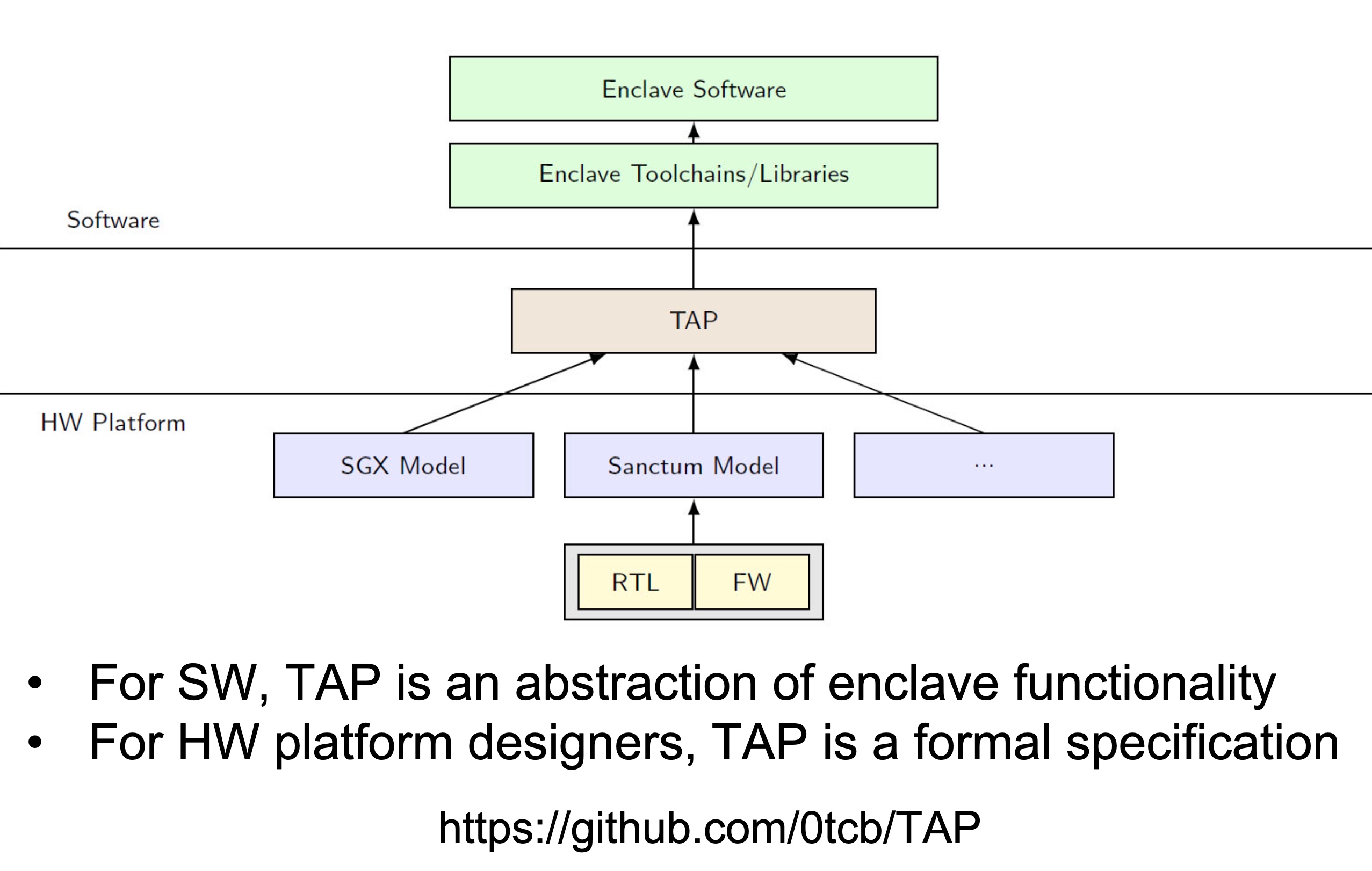
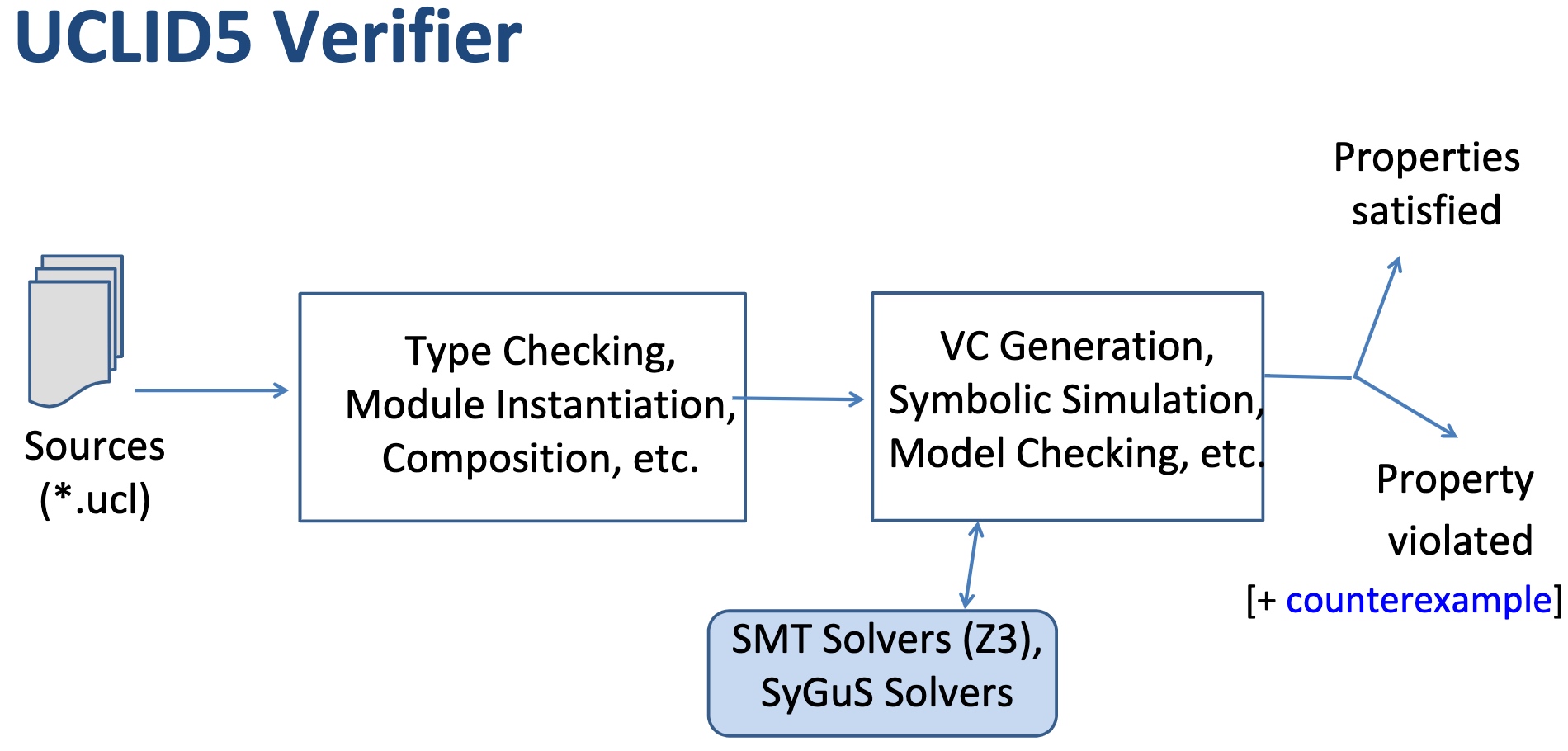
UCLID5 verifier


Modules, like LLVM, serve as the unit of re-use when declaring commonly used types, symbolic constants, and uninterpreted functions. The module uses uninterpreted functions to model instruction decoding (inst2op, inst2reg0 etc.) and instruction execution (aluOp and nextPC). Further, the register file index type (regindex_t) and the address type (addr_t) are both uninterpreted types. This abstraction is sufficient to model all kinds of CPU implementation.

Structure of the CPU Model:

  1. Module common: serves as top-level type definition.
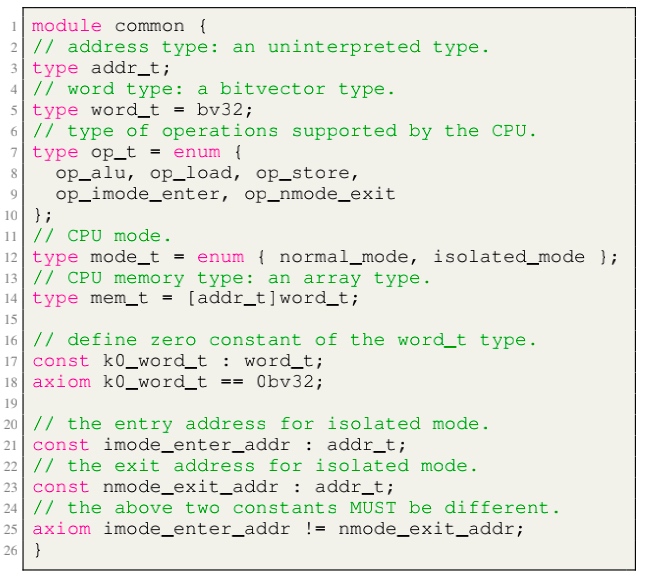
  2. Module cpu: defining the initial sate like reg/pc/imem/dmem, types are mode_t(isolated/normal) word_t addr_t(a range of addresses between isolated_rng_lo and isolated_rng_hi) init/next/exec_inst defines the transition system.
  3. Module main: the environmental assumptions for the verification and contains a proof script that proves, via induction, a 2-safety integrity property for the CPU module.

Other features

  1. Term-Level Abstraction: In term-level abstraction, concrete functions or functional blocks are replaced by uninterpreted functions or partially-interpreted functions. Concrete low-level data types such as Booleans, bit-vectors, and finite-precision integers are abstracted away by uninterpreted symbols or more abstract data types (such as the unbounded integers).
  2. Blending Sequential and Concurrent System Modeling:
  3. Diversity in Specification
    1. Procedure specifications.
      1. Invariant
      2. while
      3. assume
      4. assert
    2. LTL
    3. Hyperproperties(k-safety): composing k copies of the system together and specifying a safety property on the resulting composition
  4. Modularity in Modeling and Specification
  5. Counterexample Generation
  6. Modular Proof Scripting

More for extended reading

  1. https://www.hillelwayne.com/post/hyperproperties/https://www.cs.unc.edu/~csturton/courses/verifiedsec/lecturenotessp17/notes_lbarnett.pdf
Posted on

[Program Analysis] Soundiness and soundness

In defense to a situation where no program analysis in the program is soundness, so given term soundness for that program claims that they can cover most cases.

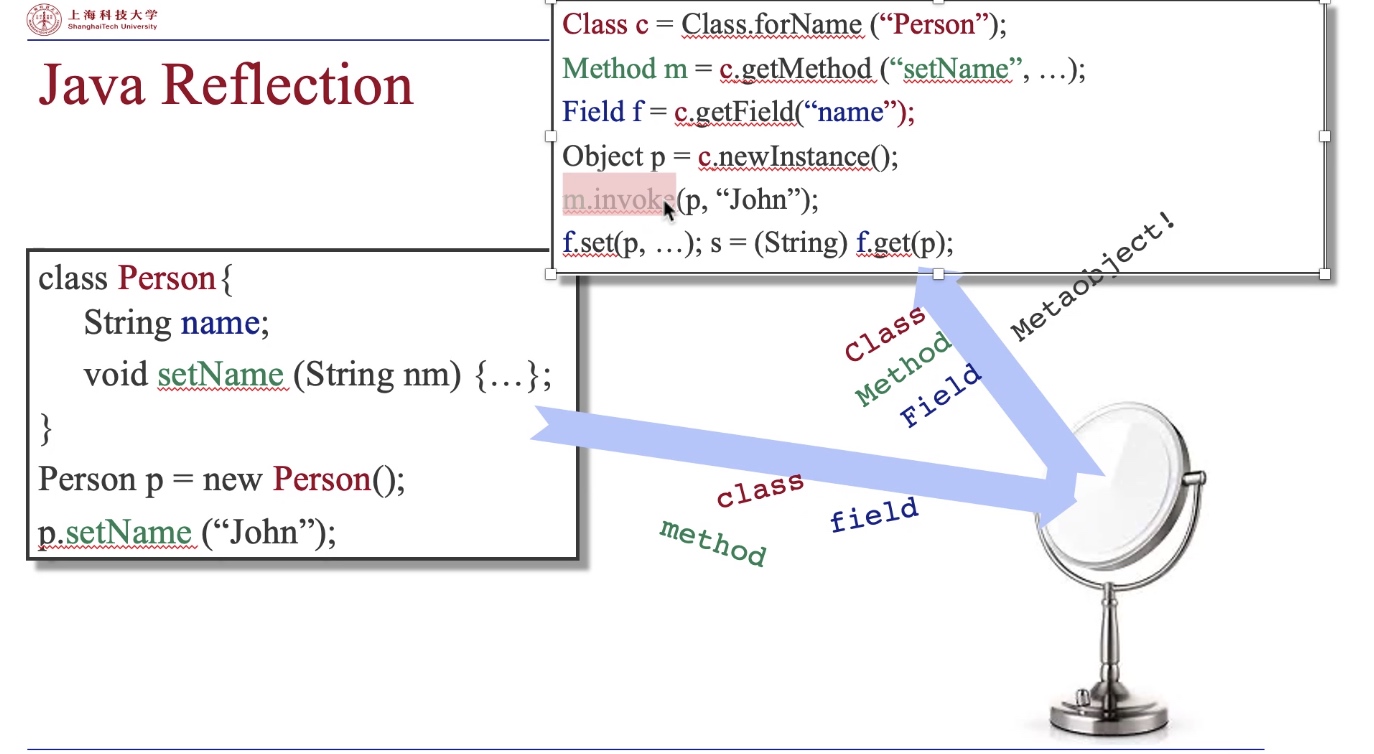
Reflection in Java

First on Java reflection: Class + Method + Field Metaobject

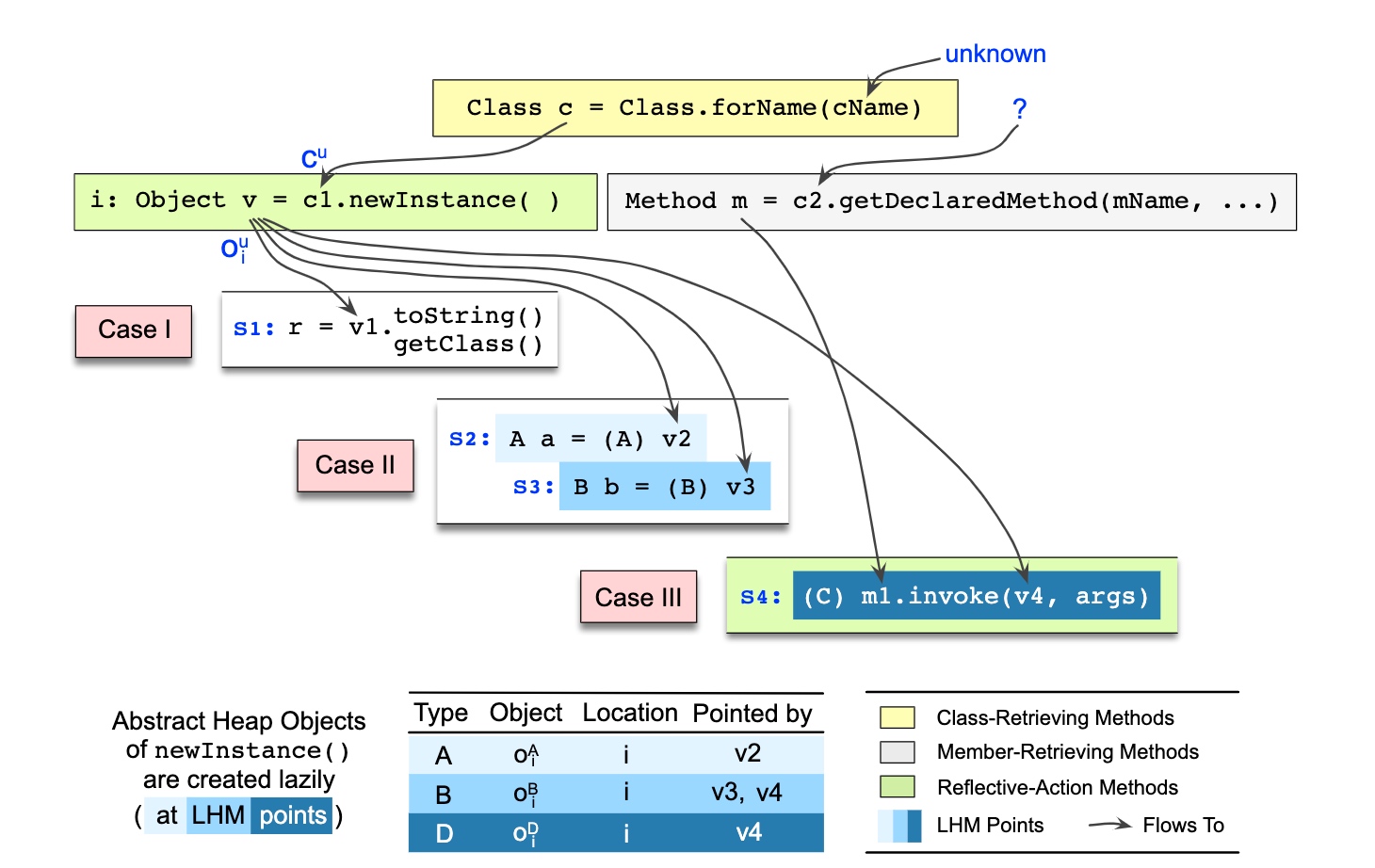
  1. One solution: String Constant analysis + Pointer Analysis
  2. List and Array propagation

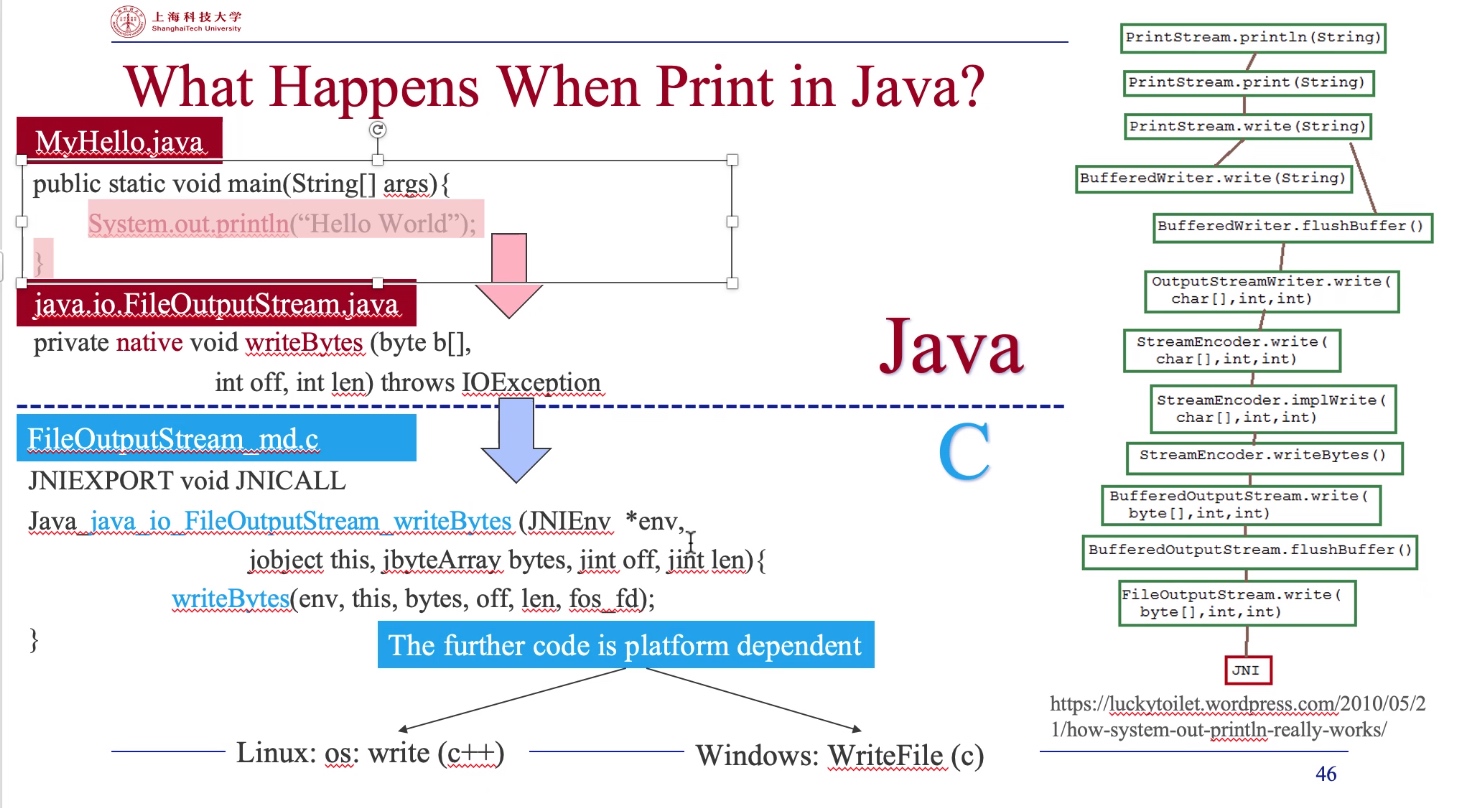
JNI Call

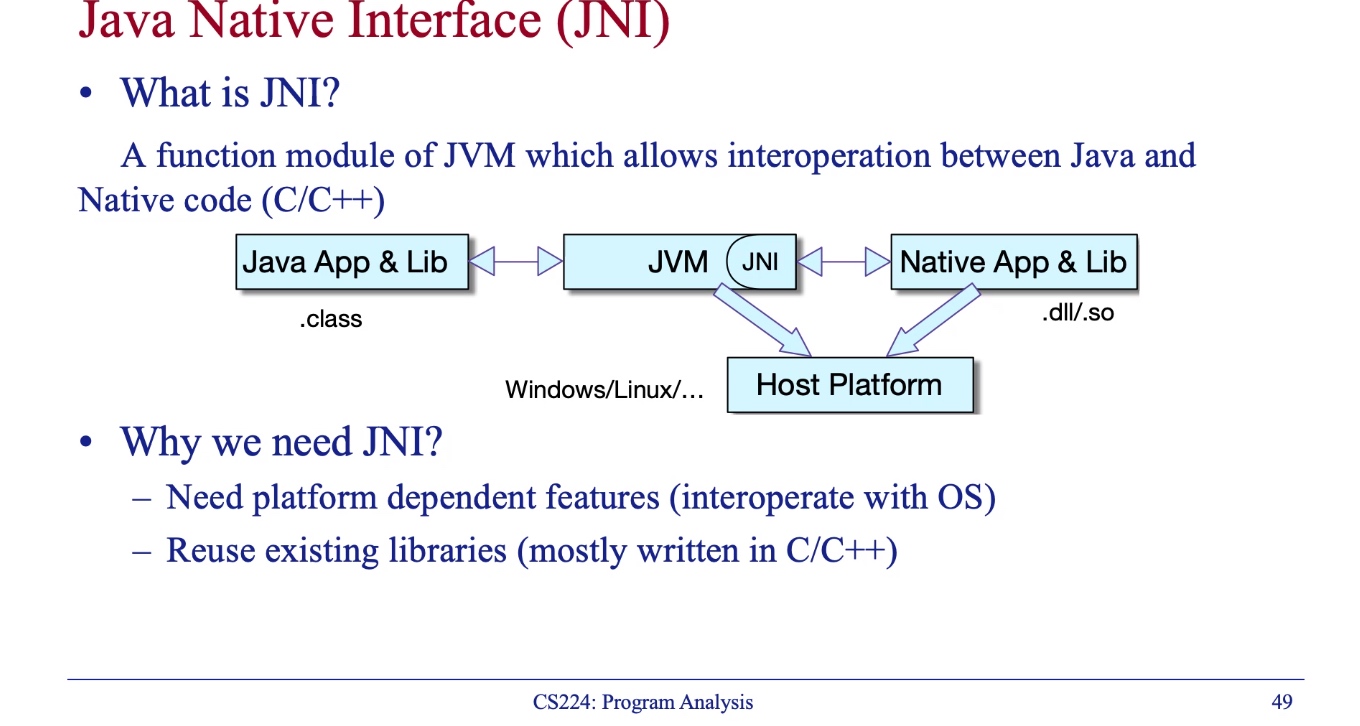
  1. One Solution: Transcode from C to Java
  2. scanning on the binary
Posted on

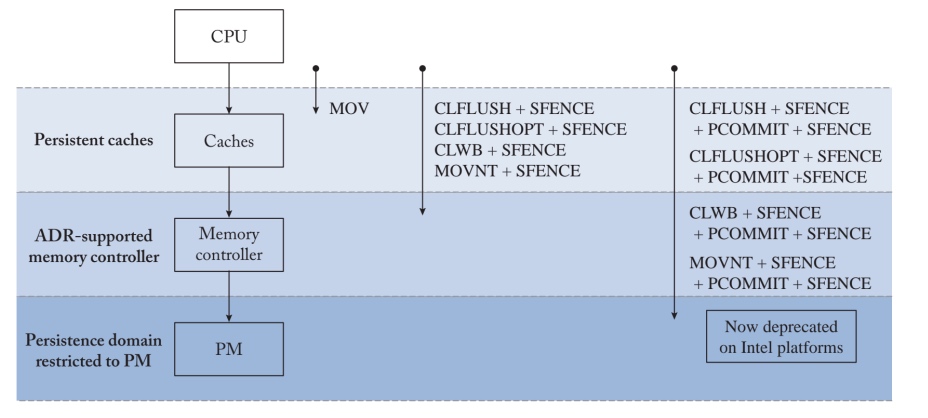
[A Primer on Memory Persistency] Persistent Memories阅读笔记

本篇是《A Primer on Memory Persistency》这本书的中文阅读笔记，会整理出我认为重要的部分。当年看《A Primer on Memory Consistency and Cache Coherence》的时候，被其对内存的描述惊艳到了，也是我对内存提起兴趣的最重要的原因。上CA2的时候对这几本书翻了又翻。

Continue reading "[A Primer on Memory Persistency] Persistent Memories阅读笔记"
Posted on

[Program Analysis] Static Analysis for Security

Like symbolic execution, Taint-Analysis is an important tool for analyzing code security vulnerabilities and detecting attack methods. Taint-Analysis can effectively detect a large number of security vulnerabilities in Web applications, such as cross-site scripting attacks, SQL injection, etc. The taint propagation technique is an important topic in the field of Taint-Analysis, which is combined with the static program analysis technique to obtain more efficient and accurate analysis results by analyzing the interdependencies between program variables without running the code and modifying the code.

Taint analysis tracks how tainted data flow through the program and observes if they can flow to locations of interest (call sinks).

Posted on

[Program Analysis] Inter-procedural Dataflow Analysis

The IFDS published at POPL'1995 is a leaf-frog jump after the classical intra-procedural analysis. Since it 1. linear time for specific individual problem 2. linear time for the locally separable problem(gen/kill bitvec) 3. Nonlinear time for other common problems.

CFL reachability

Feasible and Realizable Paths

Paths in CFG that do not correspond to actual executions is Infeasible paths. If we can prevent CFG from being contaminated by infeasible paths as much as possible and make the analysis flow graph edges more concise, we are bound to greatly improve the analysis speed. But in practice, such infeasible paths are often undecidable.

Realizable Paths

The paths in which "returns" are matched with corresponding "calls".Thus we can make the target wider. If we call one path of, the returned edge can correctly pattern matching the call-edge, we call the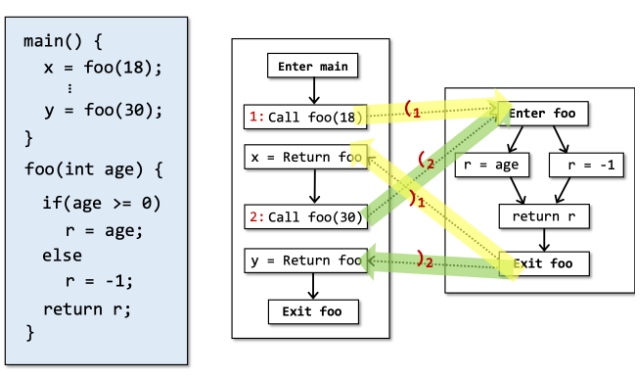

B is CFL reachable from A if there's a path (a series of edges) between two nodes A and B and all the label of the edges on this path are legal words defined by a pre-specified context-free language.

Partially Balanced-Parenthesis Problem

The search for realizable paths is abstracted into the typical bracket matching problem. Partially here means that there must be an (i match for (i. In other words, for every return-edge there is a call-edge match, but every call-edge does not necessarily have a return value (e.g., realizable but not infeasiable paths). The problem is modeled as follows: all edges on the control-flow graph are given a label, and for a call statement i, the call-edge is labeled (i and its return-edge is labeled) i, while all other edges are labeled e.

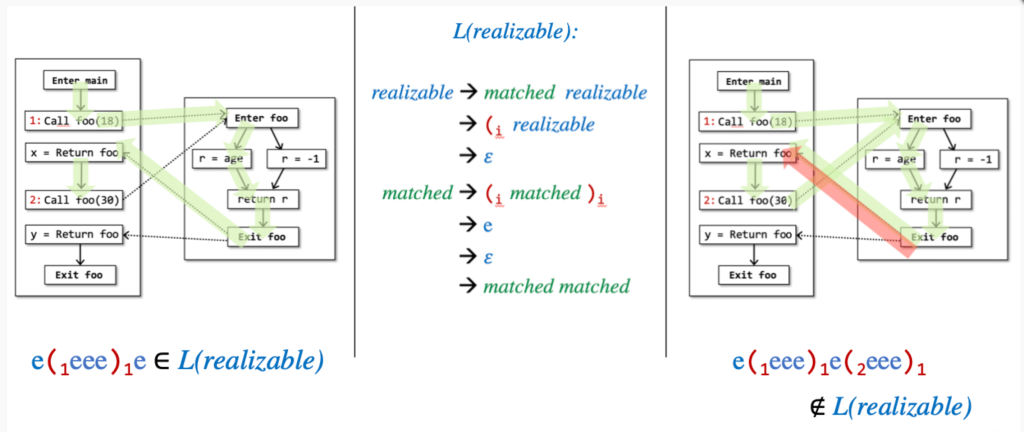
A path is a realizable path if thee path' word is in the language L(realizable).

IFDS

IFDS is for interprocedural data flow analysis with distributive flow functions over finite domains. It transforms a large class of data flow analysis problems into graph reachability problems by providing polynomial-time accuracy compared to the iterative data flow framework with the following constraints:

  1. Many general dataflow analysis problems are subset problems but interprocedural is full program analysis. The distributive flow function within the finite domain is required for IFDS.
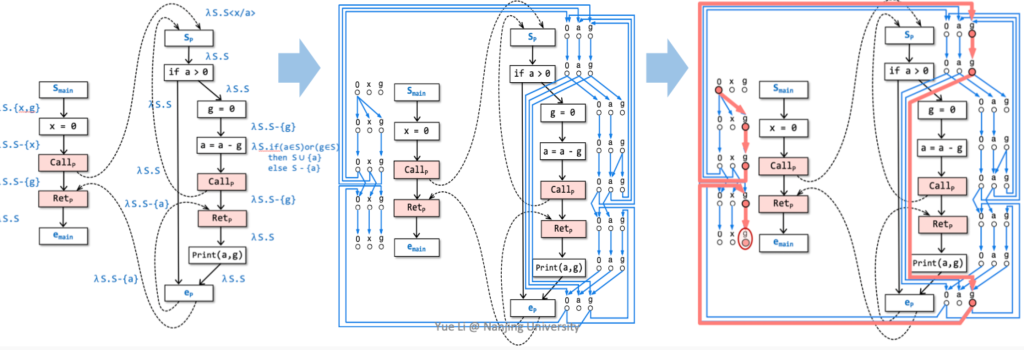
MRP

IFDS uses meet-over-all-realizable-path

to measure its analysis accuracy.
According to the definition of $M O P_{n}=\sqcup(p \in P a t h s(s t a r t, n)) p f_{p}(\perp)$, for each node point $n, M O P_{n}$ denotes the union/intersection operation of all paths from the start point to the node point n on the CFG.
And according to the definition of MRP $M O P_{n}=\sqcup(p \in P a t h s(s t a r t, n)) p f_{p}(\perp)$ , for each node point $n, M R P_{n}$ denotes all realizable paths from the start point to the node point n on the CFG (the label of these paths constitutes the word that matches the realizable label of these paths conforms to the context-independent grammar of the realizalble language) for the union/intersection operation. The result is also more accurate than $M O P_{n}$. $M R P_{n} \leqslant M O P_{n}$.

Algorithm

IFDS Algorithm:

Input: Program and the Data Flow Analysis $O$

Reference

  1. https://haotianmichael.github.io/2021/06/06/NJU%E9%9D%99%E6%80%81%E7%A8%8B%E5%BA%8F%E5%88%86%E6%9E%90-5-IFDS/
  2. https://apps.dtic.mil/sti/pdfs/ADA332493.pdf
  3. https://minds.wisconsin.edu/bitstream/1793/60188/1/TR1386.pdf
Proudly powered by WordPress