The IFDS published at POPL'1995 is a leaf-frog jump after the classical intra-procedural analysis. Since it 1. linear time for specific individual problem 2. linear time for the locally separable problem(gen/kill bitvec) 3. Nonlinear time for other common problems.
CFL reachability
Feasible and Realizable Paths
Paths in CFG that do not correspond to actual executions is Infeasible paths. If we can prevent CFG from being contaminated by infeasible paths as much as possible and make the analysis flow graph edges more concise, we are bound to greatly improve the analysis speed. But in practice, such infeasible paths are often undecidable.
Realizable Paths
The paths in which "returns" are matched with corresponding "calls".Thus we can make the target wider. If we call one path of, the returned edge can correctly pattern matching the call-edge, we call the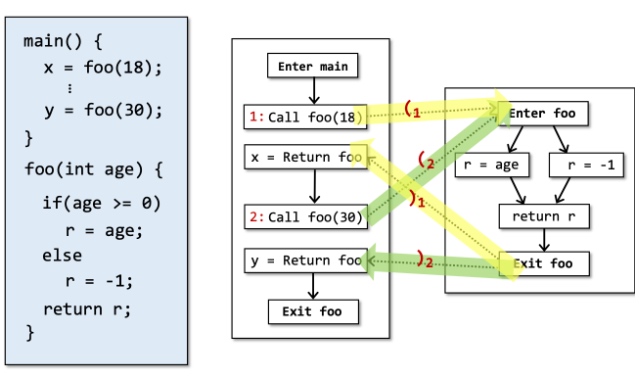
B is CFL reachable from A if there's a path (a series of edges) between two nodes A and B and all the label of the edges on this path are legal words defined by a pre-specified context-free language.
Partially Balanced-Parenthesis Problem
The search for realizable paths is abstracted into the typical bracket matching problem. Partially here means that there must be an (i match for (i. In other words, for every return-edge there is a call-edge match, but every call-edge does not necessarily have a return value (e.g., realizable but not infeasiable paths). The problem is modeled as follows: all edges on the control-flow graph are given a label, and for a call statement i, the call-edge is labeled (i and its return-edge is labeled) i, while all other edges are labeled e.
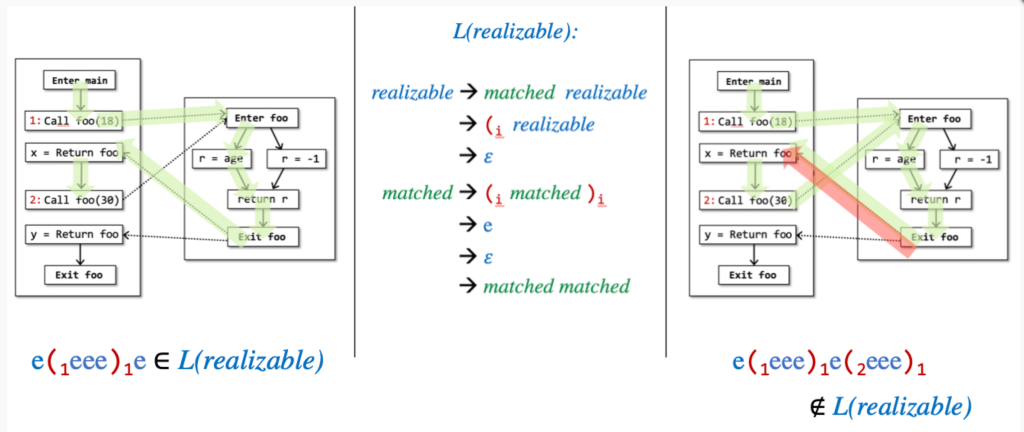
A path is a realizable path if thee path' word is in the language L(realizable).
IFDS
IFDS is for interprocedural data flow analysis with distributive flow functions over finite domains. It transforms a large class of data flow analysis problems into graph reachability problems by providing polynomial-time accuracy compared to the iterative data flow framework with the following constraints:
- Many general dataflow analysis problems are subset problems but interprocedural is full program analysis. The distributive flow function within the finite domain is required for IFDS.
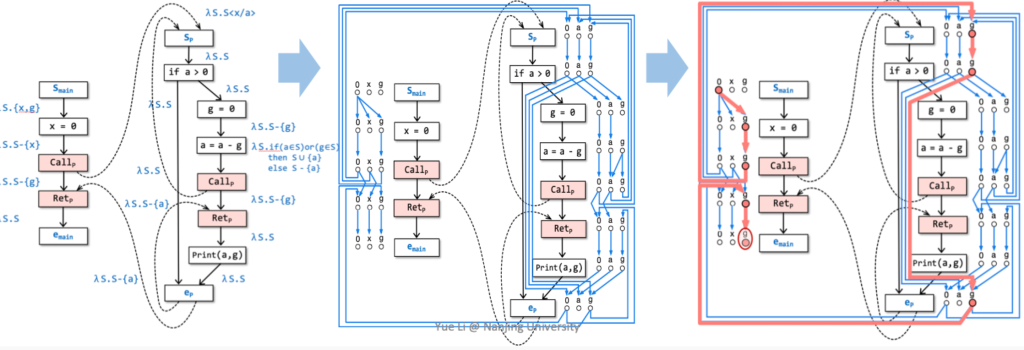
MRP
IFDS uses meet-over-all-realizable-path
to measure its analysis accuracy.
According to the definition of $M O P_{n}=\sqcup(p \in P a t h s(s t a r t, n)) p f_{p}(\perp)$, for each node point $n, M O P_{n}$ denotes the union/intersection operation of all paths from the start point to the node point n on the CFG.
And according to the definition of MRP $M O P_{n}=\sqcup(p \in P a t h s(s t a r t, n)) p f_{p}(\perp)$ , for each node point $n, M R P_{n}$ denotes all realizable paths from the start point to the node point n on the CFG (the label of these paths constitutes the word that matches the realizable label of these paths conforms to the context-independent grammar of the realizalble language) for the union/intersection operation. The result is also more accurate than $M O P_{n}$. $M R P_{n} \leqslant M O P_{n}$.
Algorithm
IFDS Algorithm:
Input: Program and the Data Flow Analysis $O$
Reference
- https://haotianmichael.github.io/2021/06/06/NJU%E9%9D%99%E6%80%81%E7%A8%8B%E5%BA%8F%E5%88%86%E6%9E%90-5-IFDS/
- https://apps.dtic.mil/sti/pdfs/ADA332493.pdf
- https://minds.wisconsin.edu/bitstream/1793/60188/1/TR1386.pdf