文章目录[隐藏]
The CHA Analysis overly pursues the speed and gives some false positive cases. For must analysis like constant propagation, it's not acceptable. Pointer Analysis computes an over-approximation of the set of which memory locations (objects) a pointer can point to.
Other than basic information like Call Graph, the pointer analysis is widely used in the compilation optimization like Alias Analysis(two object points to the same object) the robustness of the software, and security.
Intro
It's a may analysis. The input is the whole program and the result is a series of points-to relations like maps of pointing.
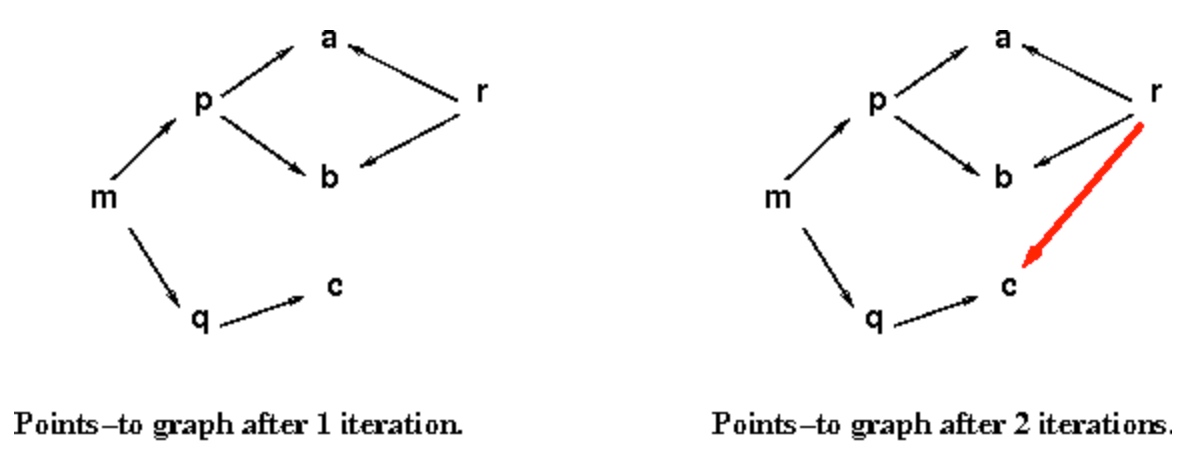
A typical testcase:
p = &a;
p = &b;
m = &p;
r = *m;
q = &c;
m = &q;

The trade-off between precision and speed depends on Heap Abstraction, Context Sensitivity, Flow Sensitivity, and Analysis Scope
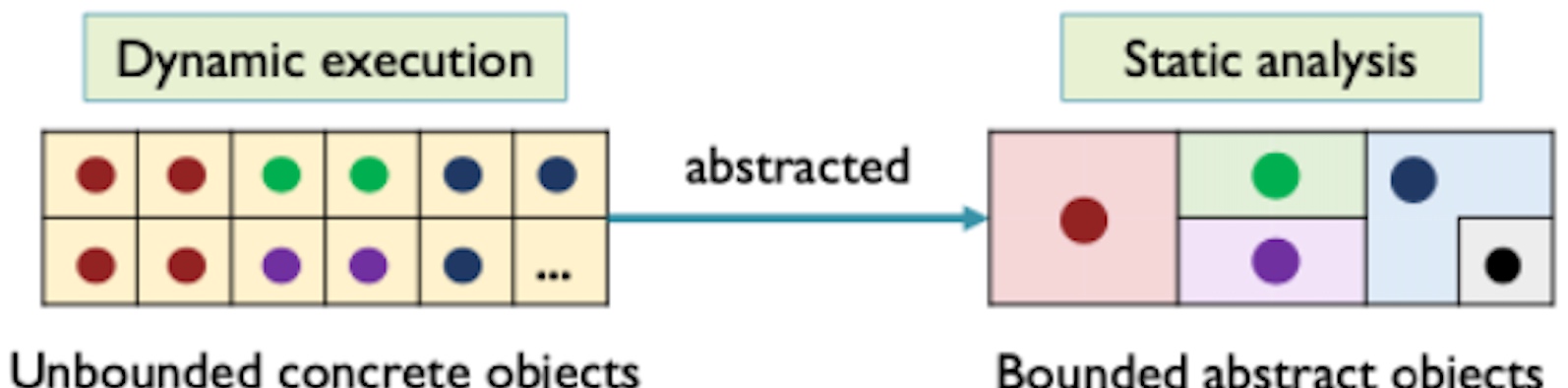
Heap Abstraction
How to abstract the operations on the heap like the loops and recursion may dynamically incur many heap objects. The unbonded operations can be abstracted to the finite static object to analyze.
class Person{
int id;
String name;
public Person(int id,String name){
this.id = id;
this.name = name;
}
}
public class PeresonMain{
public static void main(String[] args){
int id=0;
String name = "John";
for (;id<100;id+=1){
Person person = new Person(id,name);
}
}
}
The heap of new Person will be dynamically allocated, and the bound of the loop should be considered when doing the abstraction.
Context Sensitivity
It decides the precision to the greatest extent. When a function call is triggered, a context will be created. A method called multiple times will also be considered one by one for the context. In terms of sensitivity grade, the insensitivity means all calls for one method are considered once, while the context is analyzed every time is context-sensitive.
Flow Sensitivity
The control flow abstraction is all about the execution order and non-execution order consideration. The former maintains a points-to relation map for every program point. The current effectiveness of flow sensitivity to OOP language like java is undecided.
Analysis Scope
Whether to analyze the entire program directly or to analyze specific program segments driven by requirements. In fact, if there are many requirements, the complexity of analyzing them individually is comparable to that of analyzing the whole program directly
Pointers in Java
All the possible pointer declarations.
Local variable:xStatic field: C.fInstance field: x.fArray element: array[i]
The static field is a global variable and the last array element can omit the index. So we only need to consider the first 2 categories.
Pointer-Affecting Statements
In terms of the statements themselves, such as if/for/break, the control flow does not affect the results of pointer analysis; we need to focus on the real pointer-affecting statements as follows.
- New: x = new T()
- Assign: x = y
- Store: x.f = y
- Load: y = x.f
- Call: r = x.k(a, ...), especially virtual calls
Domains and Notations
Variable: $x, y \in V$
Fields: $f, g \in F$
Objects: $O_i, O_j \in O$ (Allocation sites)
Instance fields: $o_i$.f, $o_j$.g $\in O \times F$
Pointers: Pointer $=V \cup(O \times F)$
Object and Fields refer to the creation point of the allocated heap object and the fields in the abstract heap object, respectively - the combined object and field Instance Fields also represent a pointer in the program. Pointers refer to all variable and instance fields in the program.
Finally, the pointing relation pt (which is itself a mapping, representing the set of possible objects that a pointer can point to) is introduced.
- Points-to relations: pt: Pointer ⟶ 𝓟(O)
- 𝓟(O) denotes the powerset of object O
- pt(p) denotes the set of pointing relations of pointer p
The formal definition of the Pointer-Affecting Statements.
$$\begin{array}{cccc}
Kind & Statement & Rule & PEG\text{ }Edge
\end{array}$$
$$\begin{array}{cccc}
New & i: x=\text{ new }\mathrm{T}() & \overline{o_{i} \in p t(x)} &N/A \end{array}$$
$$\begin{array}{cccc}
Assign & x=y & \frac{o_{i} \in p t(y)}{o_{i} \in p t(x)} & x\leftarrow y \end{array}$$
$$\begin{array}{cccc}
Store & x . f=y & \frac{o_{i} \in p t(x), o_{j} \in p t(y)}{o_{j} \in p t\left(o_{i} . f\right)} & o_i.f\leftarrow y
\end{array}$$
$$\begin{array}{cccc}
Load & y=x . f & \frac{o_{i} \in p t(x), o_{j} \in p t\left(o_{i} . f\right)}{o_{j} \in p t(y)} & y \leftarrow o_j.f
\end{array}$$
- New: The oi in the New rule represents an object created by the Allocation site at this point, so how does the pointer analysis handle a New statement-that is, having x point to oi after the statement is executed, i.e., oi ∊ pt(x).
- Assign: If oi belongs to the pointing set of y, then after executing this statement oi needs to be added to the pointing set of x.
- Store: Save the new object to a domain f of that object - if x points to oi and y points to oj, then oi.f needs to point to oj after this statement is executed.
- Load: Load the domain f of an object into the new object - if x points to oi and oi's domain f point to oj, then add oj to the set of pointers to y after executing this statement.
Implementation
Essentially, pointer analysis is to propagate points-to information among pointers(variables & fields).
Pointer Flow Graph(PFG)
PFG is the points to information Directed graphs between pointers. The above chart shows the propagation rule, basically passing the closure by PFG showing from point A to B is data reachable. Notably, when updating the instance fields' points-to relation, the info is gained by the field and object's allocation update. Thus the process is dynamically updated. (they are mutually dependent)
Algorithm
- S: the set of statements of the input program
- WL: work list storing the pair of pointing relations to be processed, where each item <n,𝓟(O)>* means that the information in 𝓟(O) needs to be passed to the set of pointing relations pt(n) in n.
- PFG: a directed graph that represents the set that becomes an edge, where s$\rightarrow$t means that the pointing relation of s flows to the pointing relation of tH
- ybrid-Set: used to exist pt(s), i.e., when the elements are less than 16 with a HashSet greater than 16 with a BitVector.
Differential Propagation
The pt(n) information on the vertex of PEG has been propagated, so the diff is summarized when store and load which the following only check the newly added object.
Fixed Point
The algorithm conforms to the immobility principle - the function of WL is to add information to pt, and the core pt(n) ⋃ = pts after if directly check whether the pt set has changed before and after the merge also to determine whether the immobility point is reached.
!WIP